23 L’analyse en composantes principales
23.1 Le principe
Les méthodes d’ordination que nous verrons dans ce chapitre et les deux suivants (Chapitre 24 et Chapitre 25) fonctionnent toutes sur le même principe. Vous allez voir que cela est plutôt abstrait au début, mais au moment où ça clique, on réalise la puissance et la simplicité de cette approche. Ne stressez pas trop si au terme du cours le fonctionnement des ordinations est encore un peu flou dans vos têtes. Personnellement, je ne les ai vraiment comprises qu’une fois à la maîtrise. L’important sera surtout de savoir bien les appliquer et les interpréter.
Les ordinations partent de notre matrice de données originale, et la transforment en une nouvelle matrice contenant autant de variables que l’originale. Cependant, contrairement à notre matrice originale, les variables composant cette nouvelle matrice seront toujours entièrement orthogonales (i.e. non corrélées les unes avec les autres). Cela en soit peut être utile dans certaines situations, mais ce qui est surtout intéressant des ordinations est qu’elles rassemblent (ou résument) la variabilité (e.g. la variance) de nos données dans les premières variables de la nouvelle matrice.
Cela veut dire que si par exemple nous avions besoin de 30 variables pour décrire une observation dans notre matrice de données originale (dans la vraie vie, ça arrive plus souvent qu’on le voudrait!), avec une ordination, on pourrait potentiellement réduire ce nombre à 3 ou 4. Cela simplifie grandement les interprétations et les analyses subséquentes. On pourrait constater que plusieurs variables étaient redondantes, etc. Les ordinations sont donc, avant tout, des méthodes de simplification des données. Il s’agit là de la clé importante pour bien saisir les ordinations.
Ces méthodes ne cherchent PAS de lien cause à effet, elles ne trouvent pas d’explication, elle ne regardent pas de différence entre des groupes, etc. Elles ne font que réorganiser et simplifier les données.
Voici à titre d’illustration quelques bonnes questions associées à des ordinations :
- Est-il possible de résumer les caractéristiques du sommeil des mammifères en un nombre réduit de variables, ce qui faciliterait leur interprétation?
- Existe-t-il des patrons (ou des tendances etc.) dans les variables décrivant le climat des villes canadiennes?
- Comment sont reliés les différents descripteurs du milieu forestier?
- Comment s’organisent les communautés d’oiseaux du parc national de la Mauricie
Et au contraire, voici quelques exemples de mauvaises questions, qui ne peuvent PAS se répondre à l’aide d’une ordination :
- Quels sont les facteurs reliés à la fermeture de la canopée?
- Existe-il des différences significatives entre XXXXXXXX et YYYYY
- Quelles sont les causes d’un allongement des cycles de sommeil chez les mammifères?
- La proportion de villes plus froides augmente-elle au fil du temps?
23.2 L’aspect technique
Vous vous en doutez peut-être, mais il y a une certaine logique derrière la construction de la nouvelle matrice résultant d’une analyse en composantes principales (ACP). La nouvelle matrice n’est évidemment pas générée au hasard.
La première chose à savoir est qu’il existera une recette pour passer d’une matrice à l’autre. Cette recette se nomme les eigenvector. Elle nous permet de passer de la matrice originale à la nouvelle matrice, en nous disant comment construire les nouvelles variables à partir des originales. Ces nouvelles variables, dans l’ACP, se nomment composantes principales (d’où le nom de l’analyse…). Vous verrez que l’on utilise aussi souvent le terme axe ou axe principal.
Si notre matrice originale contenait trois variables et se nommait y, l’eigenvector de la première composante principale (zi) pourrait ressembler à ceci :
\[ z_1 = 2 \times y_{1,1} - 3 \times y_{1,2} + 4 \times y_{1,3} \]
Autrement dit, pour créer la première composante principale, on prend un peu de y1, beaucoup de y3 et on soustrait du y2. Comme notre matrice originale contenait trois variables, il existera deux autres recettes semblables pour définir les composantes principales 2 et 3.
L’autre aspect important du travail de l’ACP, comme nous en avons discuté plus haut, est de rassembler la variance dans les premières composantes principales. C’est ici qu’entrent en jeu les matrices de variance-covariance et de corrélation vues au Chapitre 22. Si nous reprenons l’exemple de ce chapitre avec les poissons dont nous avions noté la longueur, le poids et la profondeur de capture, rappelez-vous que la matrice de variance-covariance ressemblait à ceci :
| Longueur | Poids | Profondeur | |
|---|---|---|---|
| Longueur | 1271,2 | -233,0 | 30,9 |
| Poids | -233,0 | 131,5 | -12 |
| Profondeur | 30,9 | -12 | 1,3 |
Au terme du calcul de l’ACP, la nouvelle matrice de variance-covariance des composantes principales ressemblerait à ceci :
| Axe 1 | Axe 2 | Axe 3 | |
|---|---|---|---|
| Axe 1 | 1317,8 | 0 | 0 |
| Axe 2 | 0 | 86,1 | 0 |
| Axe 3 | 0 | 0 | 0,1 |
C’est ici qu’il faut apprendre (encore!) un nouveau mot de vocabulaire, soit les eigenvalues. C’est le terme technique qui désigne la variance de chacune des composantes principales au terme de l’analyse. Remarquez d’abord que toutes les covariances sont à zéro : les composantes principales sont orthogonales les unes par rapport aux autres. Remarquez ensuite que l’axe 1 est celui qui possède la plus grande eigenvalue, suivi de l’axe 2 et de l’axe 3. Dans le cas présent, comme nos variables étaient peu corrélées ensemble, il n’y a pas beaucoup de différences entre l’eigenvalue de l’axe 1 et la variance de notre variable originale ayant le plus de variance (la longueur), mais parfois ces différences pourraient être énormes.
Comme nous en avons discuté dans le Chapitre 22, interpréter la matrice de variance-covariance peut souvent être trompeur à cause des différences d’échelle entre les variables. C’est pourquoi, la majorité du temps, l’ACP sera calculée non pas sur la matrice de variance-covariance, mais bien sur la matrice de corrélation. En fait, à moins d’avoir d’excellentes raisons, il faudrait toujours calculer l’ACP sur la matrice de corrélation. Soyez prudent cependant, la plupart des logiciels calculent l’ACP par défaut sur la matrice de variance-covariance et c’est à vous d’en choisir autrement.
Enfin, pour terminer cette section sur la technicalités, sachez qu’il existe deux techniques mathématiques pour calculer l’ACP à partir d’une matrice de données. On peut soit effectuer une décomposition spectrale ou soit une décomposition en valeurs singulières (SVD).
23.3 Intuition visuelle
Pour les esprits plus mathématiques parmi vous, la section précédente a peut-être suffit à saisir l’ACP. Pour le commun des mortels par contre, l’ACP est habituellement plus facile à comprendre visuellement que mathématiquement.
Pour des fins d’illustration, je travaillerai comme si notre matrice de données originale ne contenait que deux variables. Remarquez que dans la vraie vie, si vous ne travaillez qu’avec deux variables, il n’est probablement pas pertinent de faire une ACP…
Donc voilà, disons que nous avons mesuré sur une dizaine de poissons le poids et la longueur, et que nous avons obtenu les résultats suivants :
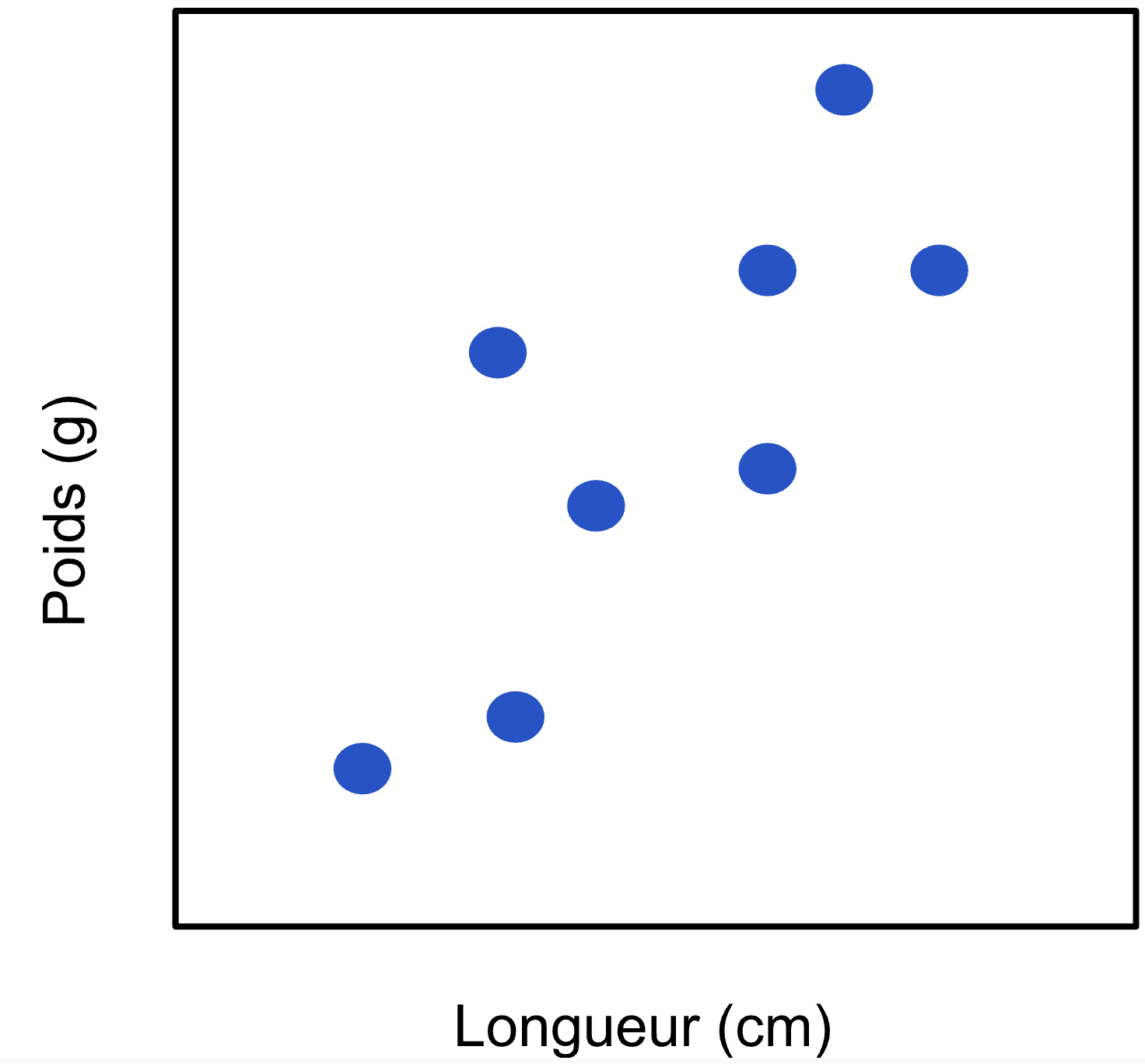
L’ACP tenterait d’abord de trouver dans ce nuage de points la façon de passer un nouvel axe, qui permettrait d’expliquer le plus de variabilité (i.e. de séparer les points le plus possible). Dans nos données, cet axe passerait probablement quelque part ici :
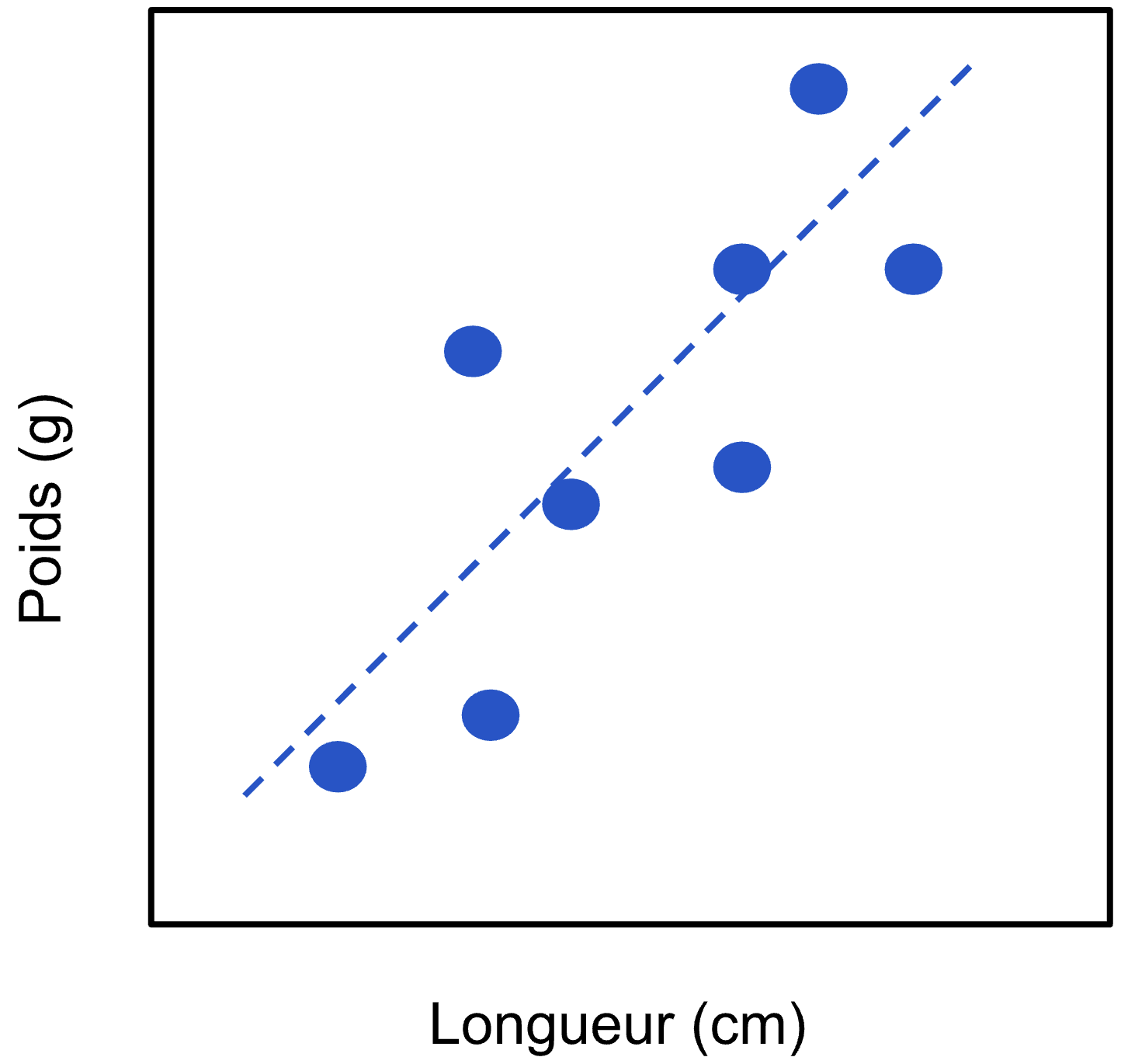
Une fois cet axe trouvé, l’ACP cherchait ensuite où passer un deuxième axe (puisque nos données originales contenaient deux variables), qui soit orthogonal au premier. Puisque nous sommes en deux dimensions, il suffit de placer cet axe à 90° du premier :
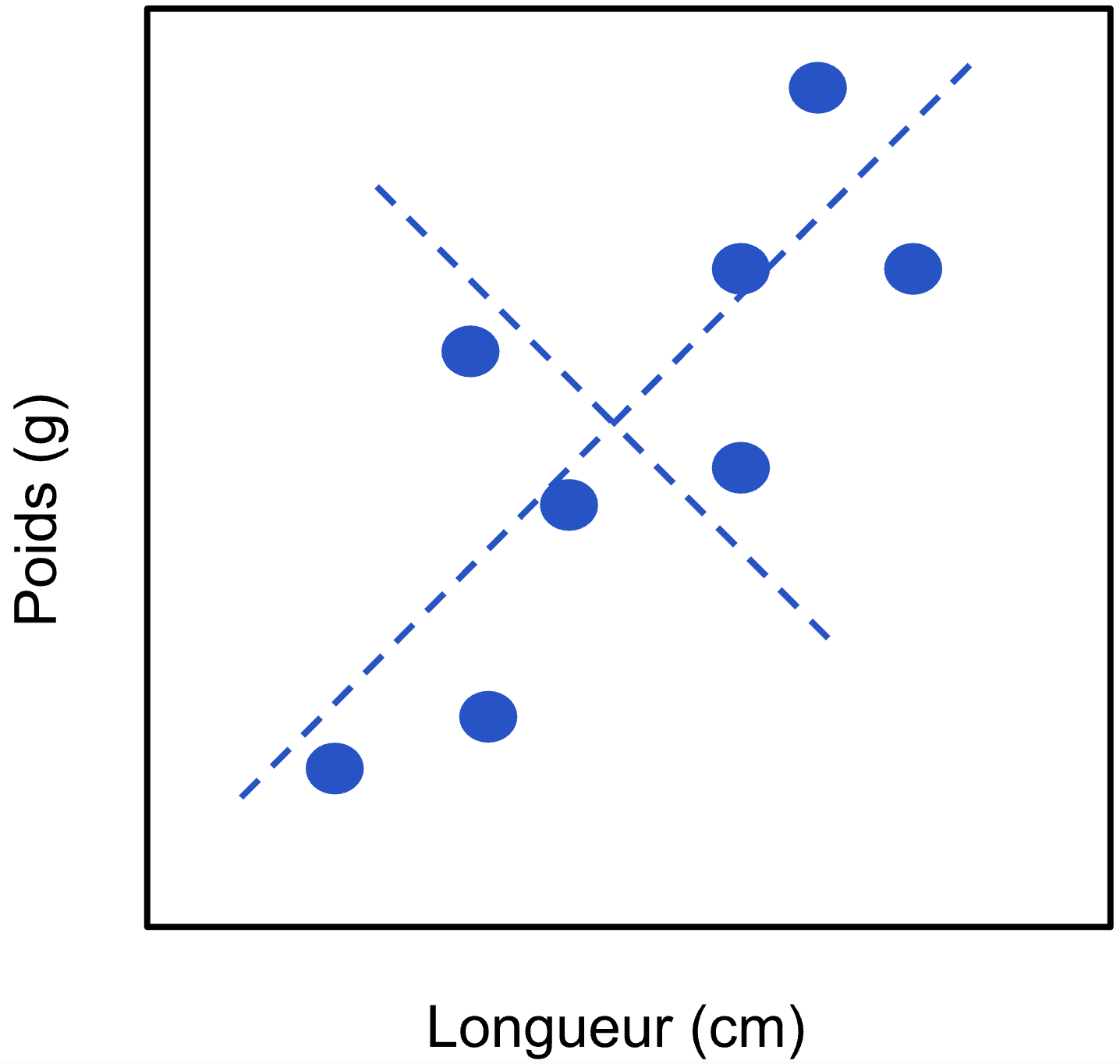
Ensuite, l’ACP fait pivoter notre nuage de points, de façon à ce que l’axe 1 de l’ACP soit bien horizontal et l’axe 2 bien vertical, comme ceci :
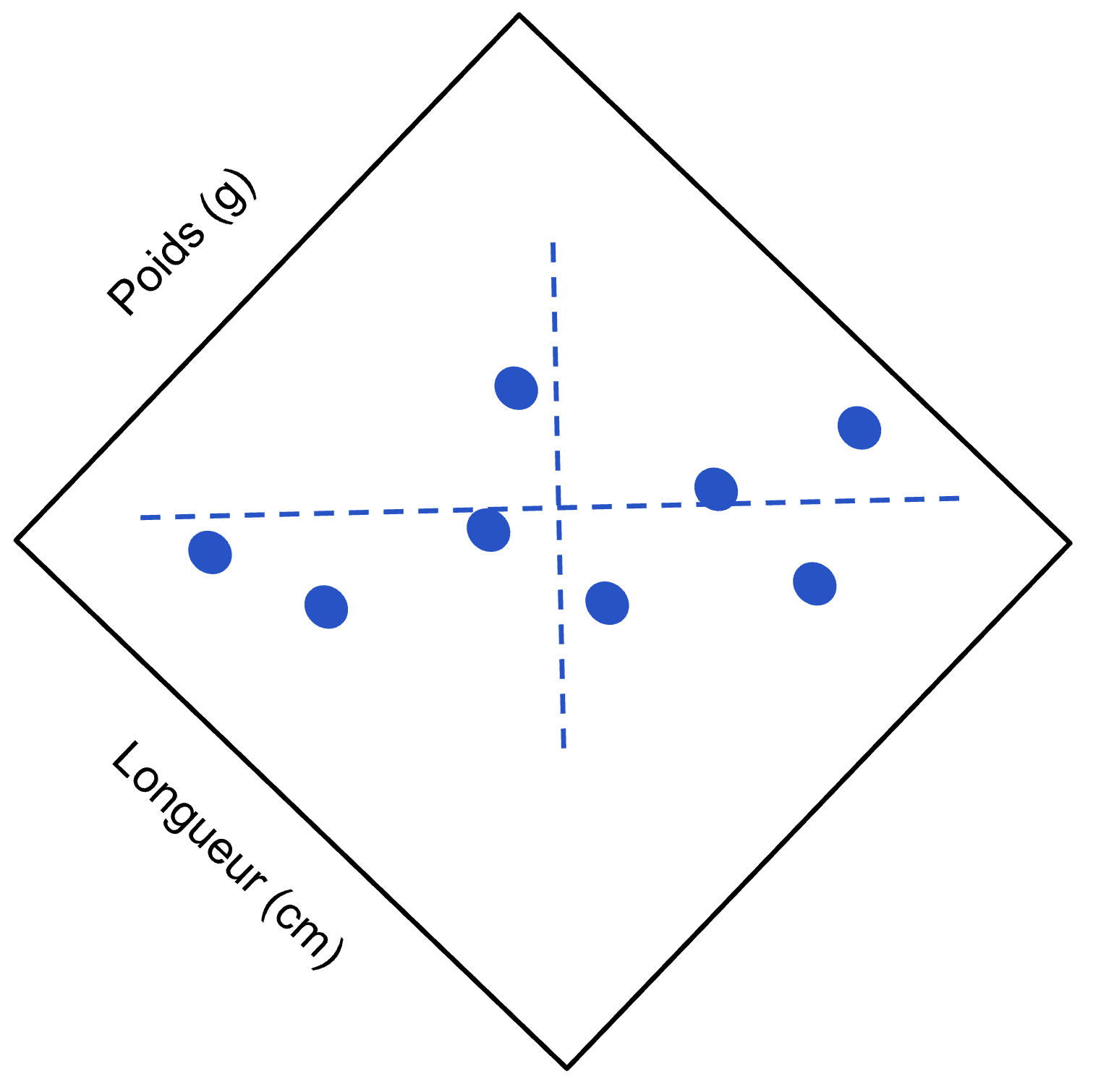
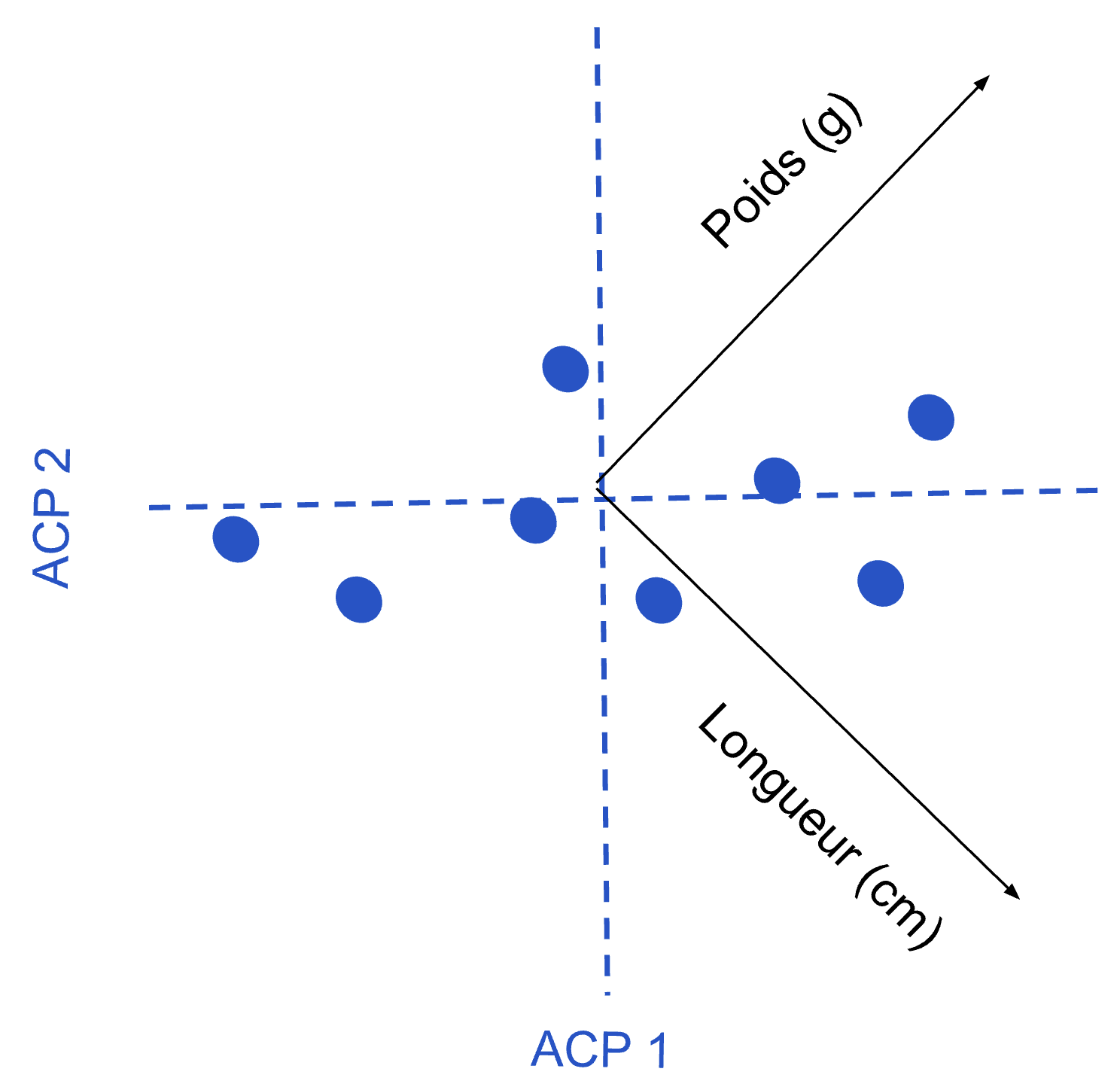
Dans ce nouveau système d’axes, défini par les composantes principales, on peut maintenant bien voir l’effet de simplification. Alors qu’au départ on avait besoin de deux variables pour définir la position d’une observation (longueur et poids), on peut voir que dans le graphique final, on pourrait essentiellement fournir uniquement la position dans l’axe 1 et que l’on perdrait très peu d’information. Remarquez que l’on peut visualiser les axes originaux (poids et longueur), pour mieux comprendre la composition des nouveaux axes. C’est la version visuelle des eigenvectors, la recette pour composer les nouveaux axes.
À ce point, ce qu’il importe de bien saisir est que contrairement à moi sur la page, l’ACP peut travailler en autant de dimensions que nécessaire. Si nous avions trois variables, elle pivoterait le nuage de points aussi sur l’axe des Z, en trois dimensions. Si nous avions 10 variables, l’analyse n’aurait aucun problème à pivoter un nuage de points en 10 dimensions. Par contre, lorsque nous tentons de visualiser les résultats avec notre œil d’humain, nous ne pouvons regarder que 2 axes de l’ACP à la fois. Si on observe par exemple une ACP faite sur 4 variables comme ceci :
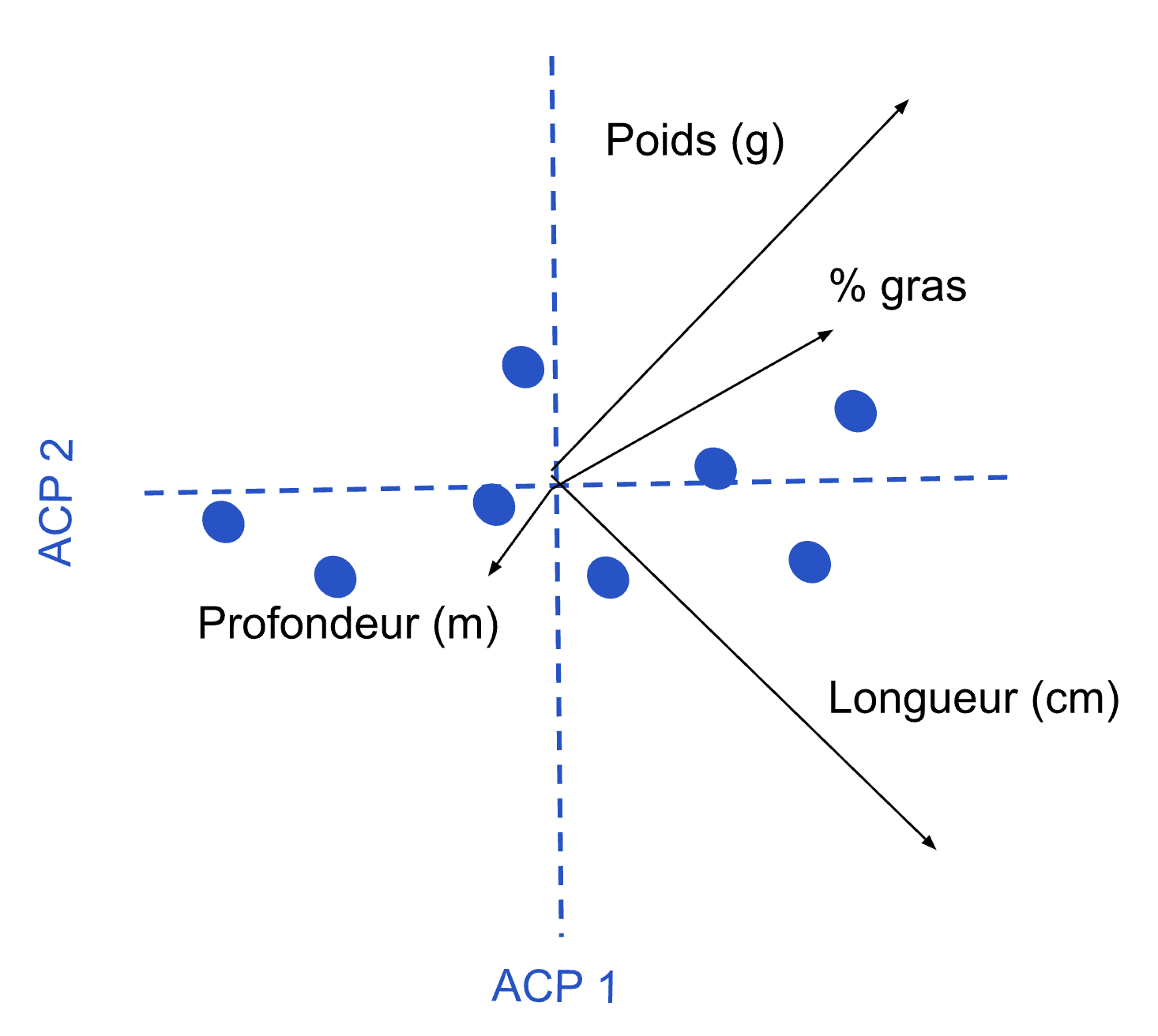
Il importe de bien comprendre que si la flèche de la variable profondeur semble courte, c’est qu’elle n’est pas très associée aux axes 1 et 2. Il faut s’imaginer qu’elle entre dans la feuille, et est probablement associée aux axes 3 ou 4 de l’analyse. De la même façon, si la flèche de la variable % gras semble plus courte, c’est qu’elle est moins associée à l’axe 1 que celles de longueur et de poids. Si on avait illustré les axes 3 et 4 de l’analyse, les résultats auraient été différents.
23.4 Mais où est la simplification?
Si vous avez réussi à suivre jusqu’ici, vous vous demandez probablement où est l’aspect de simplification dans tout cela? Si la matrice des composantes principales contient autant de variables que la matrice originale, quel est l’intérêt?
C’est ici que l’aspect subjectif d’interprétation d’une ACP entre en ligne de compte. Comme nous avons discuté, l’ACP concentre la variabilité dans les premiers axes. Il n’en reste donc que très peu dans les derniers axes. Aussi peu que, souvent, on peut simplement ignorer les derniers axes au moment de l’interprétation.
Mais combien de composantes peut-on ignorer? Il n’existe pas une seule bonne réponse parfaite à cette question. La meilleure stratégie est d’utiliser votre jugement. Aucune technique statistique ne peut vous dire ce qui est important ou non. Cependant, il existe quelques stratégies pour guider votre choix.
La première stratégie, probablement la plus simple, consiste à ne conserver pour interprétation que les axes ayant un eigenvalue > 1. Évidemment, pour appliquer cette règle, l’ACP devra avoir été calculée sur la matrice de corrélation, sinon les valeurs d’eigenvalues sont complètement arbitraires.
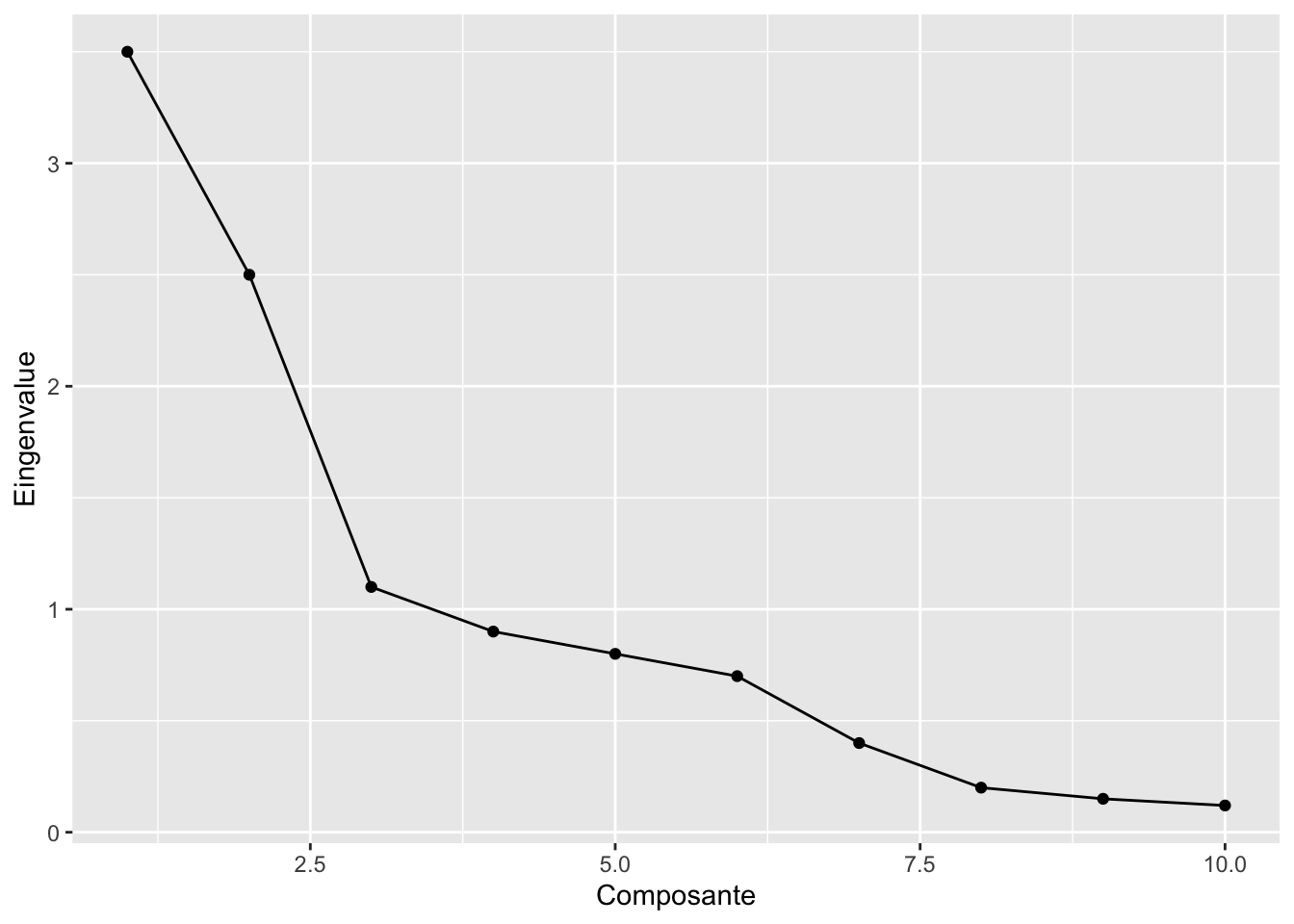
La deuxième stratégie consiste à tracer et interpréter un diagramme en éboulis (scree plot). Ce dernier est relativement simple à tracer : vous mettez en X le numéro de chacune des composantes principales, et en Y, l’eigenvalue de chacun des axes :
Avec un peu de chance, vous réussirez à trouver dans ce graphique un coude, c’est-à-dire un changement de pente, où cette dernière passe de plus abrupte à plus douce. La stratégie consiste à conserver jusqu’au point d’inflexion, inclusivement. Dans le graphique précédent, on aurait par exemple conservé les trois premiers axes.
La dernière stratégie consiste à établir un seuil de % d’explication au-delà duquel on arrête d’interpréter les axes. Pour utiliser cette technique, il faut se préparer un petit tableau, dans lequel on calcule le % cumulatif d’explication donné par l’eigenvalue de chacun des axes. Par exemple, pour notre exemple sur les longueurs de poissons, il ressemblerait à ceci :
| Axe | Eigenvalue | % expliqué | % cumulatif |
|---|---|---|---|
| ACP1 | 1317,8 | 93,86 | 93,86 |
| ACP2 | 86,1 | 6,13 | 99,99 |
| ACP3 | 0,1 | 0,01 | 100 |
Si on avait établi que l’on voulait garder tous les axes jusqu’à 90 % d’explication, on aurait conservé que l’axe 1 seulement, alors que si on avait établi notre seuil à 95 %, on aurait plutôt interprété les deux premiers axes.
23.6 Les assomptions de l’ACP
Comme toutes les techniques statistiques, l’ACP comporte certaines assomptions. La première chose à savoir est que l’ACP cherche des relations linéaires entre les variables. Donc, elle sera beaucoup plus efficace pour résumer vos données si vous prenez le temps de linéariser les relations entre vos variables à l’aide des transformations appropriées (voir Chapitre 9). Aussi, comme pour toutes les analyses, la présence de données aberrantes peut influencer le résultat de vos analyses. Ces dernières doivent donc être inspectées et gérées adéquatement.
Pour une utilisation descriptive de l’ACP comme nous le faisons dans ce cours, l’ACP n’a pas d’assomption au niveau de la distribution des variables. Cependant, si un jour vous voulez appliquer des tests statistiques sur l’ACP afin de savoir quels axes sont significatifs, etc. sachez qu’à ce moment, chacune de vos variables doit aussi suivre une distribution normale.
23.7 Labo : L’analyse en composantes principales
Pour le laboratoire de ce chapitre, nous regarderons comment s’organisent les différentes mesures morphométriques des manchots de l’archipel de Palmer.
Sachez d’abord que pour appliquer l’ACP dans R, il existe une panoplie de fonctions différentes. En général, elles arrivent toutes exactement au même résultat. Si vous n’utilisez que R de base, la fonction prcomp est tout à fait appropriée pour calculer des ACP. Cependant, comme les analyses des deux prochains chapitres nécessitent l’utilisation de la librairie vegan, je vous montrerai comment calculer vos ACP aussi à l’aide de cette librairie, afin que la façon de faire soit constante entre les différentes techniques.
La première chose à faire sera donc d’activer les librairies nécessaires :
library(vegan)Loading required package: permuteLoading required package: latticelibrary(tidyverse)Ensuite, nous nous préparerons un tableau de données ne contenant que les variables quantitives, duquel nous retirerons les lignes contenant les valeurs manquantes.
Nous conserverons dans un autre tableau le reste des informations pour pouvoir colorer nos points dans nos graphiques, par exemple selon l’espèce.
Attention, il est très important d’extraire le reste des informations après avoir éliminé les valeurs manquantes, sinon les lignes ne correspondront pas entre nos deux tableaux.
library(palmerpenguins)
Attaching package: 'palmerpenguins'The following objects are masked from 'package:datasets':
penguins, penguins_rawpour_acp <-
penguins |>
drop_na(bill_length_mm:body_mass_g)
infos_complementaires <-
pour_acp |>
select(species, island, sex, year)
pour_acp <-
pour_acp |>
select(bill_length_mm:body_mass_g)Ensuite, une façon rapide d’explorer nos données avant de commencer une analyse avec plusieurs variables et d’utiliser la fonction ggpairs de la librairie GGally. Cette dernière nous permet de voir en une seule commande l’histogramme de chacune de nos variables et le nuage de points illustrant la forme de la relation entre chacune de nos variables.
library(GGally)
ggpairs(pour_acp)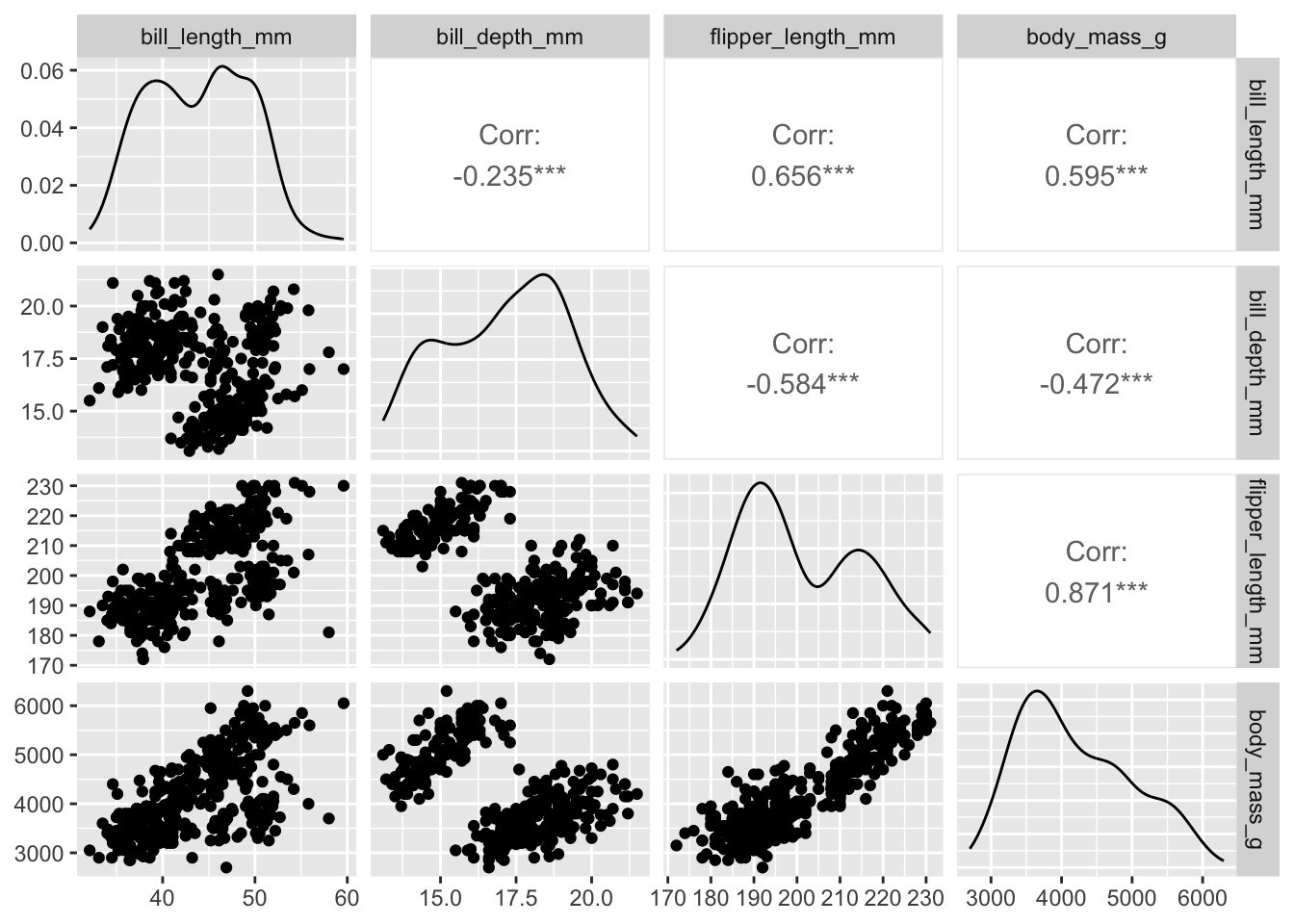
Remarquez que les histogrammes sur la diagonale sont lissés plutôt que d’afficher chacune des bandes, mais l’interprétation demeure la même.
Si jamais vous voulez remplacer les courbes de lissage par des histogrammes, on peut le spécifier directement, comme ceci :
ggpairs(pour_acp, diag = list(continuous = "barDiag"))
En général, tout cela est tout à fait OK pour l’ACP. Les distributions sont relativement normales et les relations sont relativement linéaires. Ou au moins, on ne voit pas de relations clairement non-linéaires (p. ex. exponentielle).
Ce genre de graphiques présentant l’ensemble des distributions et des relations est extrêmement pratique. Je vous conseille, au début de chaque projet d’analyse, de lancer la commande ggpairs et d’imprimer le résultat pour conserver à portée de main ce graphique, pour pouvoir y référer et en discuter avec vos collègues. On aurait même pu préparer ce graphique pour notre tableau de données original, incluant les variables catégoriques :
ggpairs(penguins)
Pour calculer l’ACP à l’aide de la librairie vegan, vous devez utiliser une fonction nommée pca (Principal Component Analysis).
Enfin, comme nos données sont à des échelles différentes, il est important de spécifier à la fonction de travailler sur la matrice de corrélation, avec l’argument scale = TRUE. Vous remarquerez enfin que plutôt que d’afficher directement le résultat du calcul, je le conserve dans un objet que je nomme acp, puisque nous aurons plusieurs petites choses à faire avec :
acp <- pca(pour_acp, scale = TRUE)La première chose que l’on peut regarder ensuite est les eigenvectors de votre ACP :
summary(acp)
Call:
pca(X = pour_acp, scale = TRUE)
Partitioning of correlations:
Inertia Proportion
Total 4 1
Unconstrained 4 1
Eigenvalues, and their contribution to the correlations
Importance of components:
PC1 PC2 PC3 PC4
Eigenvalue 2.7538 0.7725 0.36524 0.10849
Proportion Explained 0.6884 0.1931 0.09131 0.02712
Cumulative Proportion 0.6884 0.8816 0.97288 1.00000On peut y constater que le premier axe de l’ACP explique à lui seul 68% de la variation dans nos données (Proportion explained), et qu’avec trois axes, on dépasse déjà 95% d’explication (Cumulative proportion).
On peut ensuite aller observer les eigenvectors. Autrement dit, la contribution de chacune de nos variables originales à la construction des nouveaux axes de l’ACP.
Ici, on ajoute la mention 1:4 pour obtenir la construction de tous les axes (nous avions 4 varibales). Mais on aurait pu aussi en demander moins, par exemple avec 1:2.
scores(acp, choices = 1:4)$species PC1 PC2 PC3
bill_length_mm 2.295549 -1.594500048 -1.1831757
bill_depth_mm -2.018643 -2.130607173 0.7683875
flipper_length_mm 2.904483 -0.006095108 0.4261922
body_mass_g 2.764994 -0.225309318 1.0955789
PC4
bill_length_mm 0.1456481
bill_depth_mm -0.1681303
flipper_length_mm -0.7844720
body_mass_g 0.5803802Remarquez qu’il est un peu étrange d’aller chercher l’item species. Ce qu’il faut comprendre à propos des noms étranges dans vegan est que la librairie a été conçue à l’origine pour analyser des données où chaque colonne était une espèce et chaque ligne était un site. Chaque fois qu’on lit les sorties de vegan, il faut transposer les termes pour les ramener à notre jeu de données actuel. C’est emmerdant, mais au-delà de ces problèmes de noms, les qualités techniques de vegan en ont fait le standard pour les ordinations en écologie, et les choses ne semblent pas près de changer.
Donc, le tableau des eigenvectors (nommé Species scores) nous informe que les deux variables les plus associées à l’axe 1 (en valeur absolue) sont la longueur des ailes et le poids du corps, tous deux du même côté de l’axe. Les variables associées au bec sont aussi associées à cet axe, mais moins fortement.
L’axe 2 quant à lui est surtout formé des variables de longueur et épaisseur du bec, associées toutes les deux du même côté de l’axe.
On pourrait donc interpréter le premier axe comme un axe de taille du corps (des oiseaux lourds avec des grandes ailes d’un côté et petits de l’autre) et le deuxième comme un axe de taille de bec (les oiseaux avec un grand bec épais d’un côté, les petits becs de l’autre).
Si l’on veut baser (ou valider) nos interprétation sur les graphiques, on peut utiliser à cette fin la fonction biplot, à laquelle on passe notre objet de résultats, comme ceci :
biplot(acp)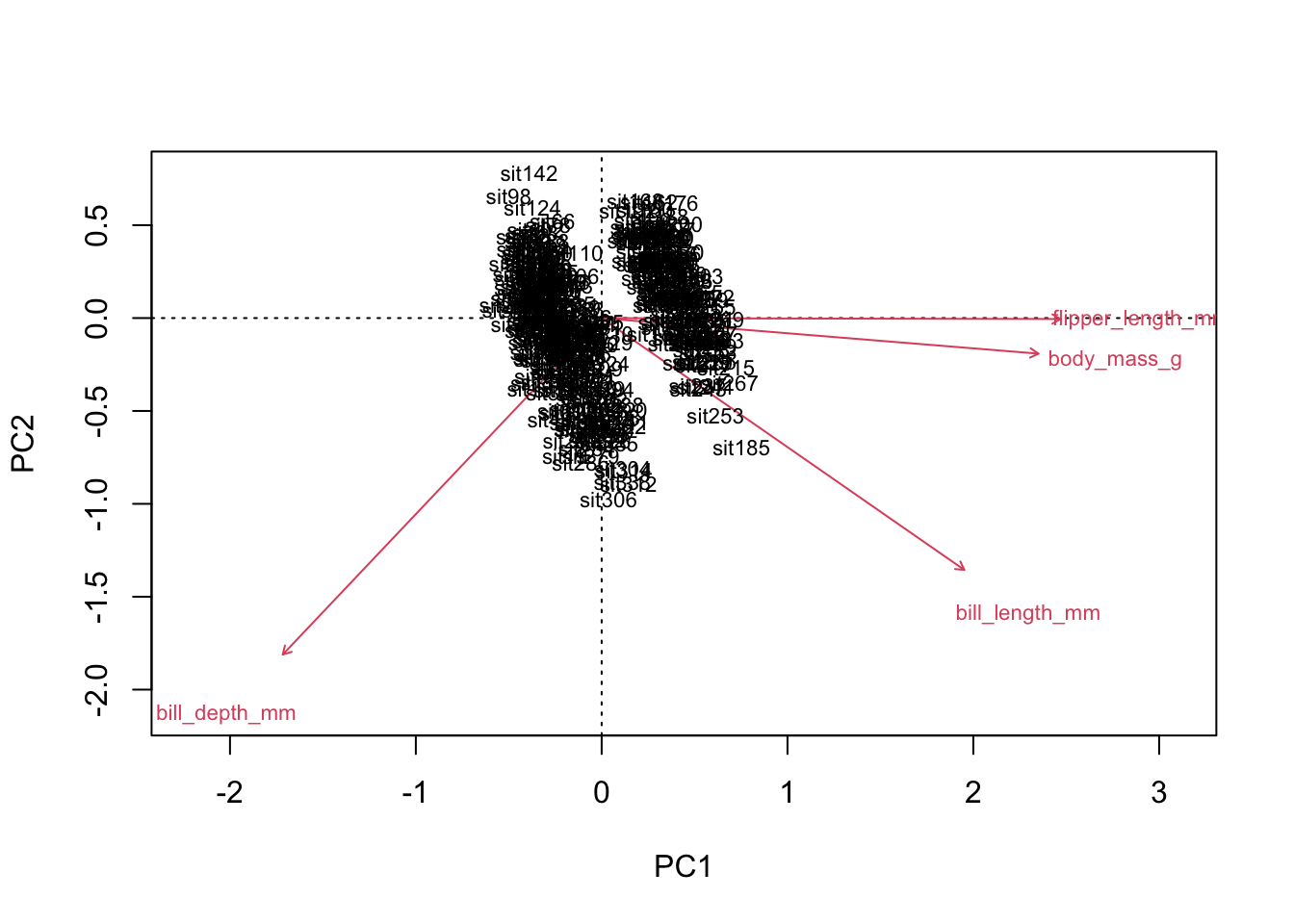
Malheureusement, ce premier graphique n’est pas très utile. Lorsque notre tableau de données contient beaucoup d’observations, la fonction biplot de vegan préfère cacher les étiquettes pour ne pas alourdir le graphique. Pour récupérer les étiquettes dans ces cas-là, il faut spécifier manuellement à la fonction que nous voulons les étiquettes :
biplot(acp, type = c("text","text"))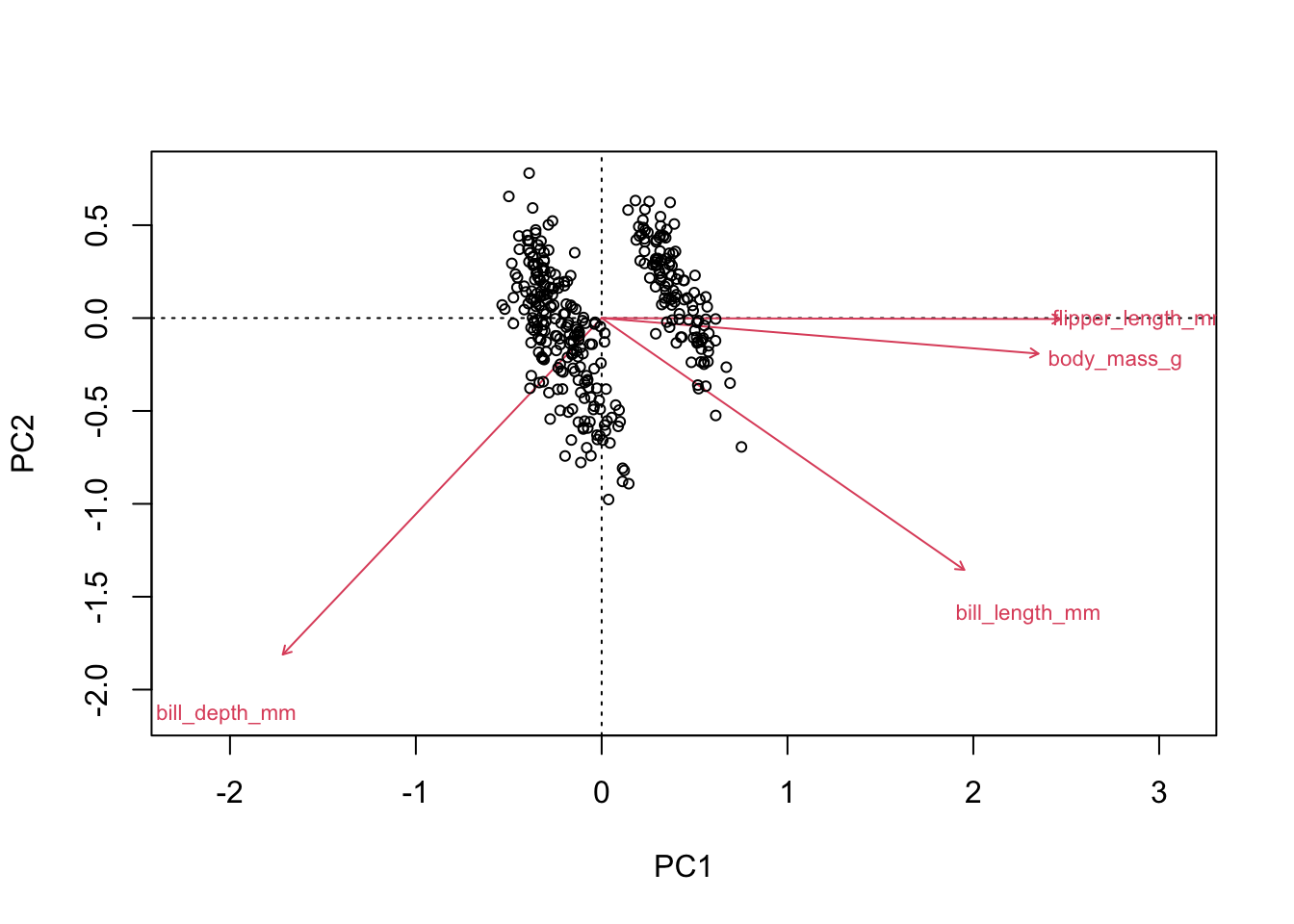
Comme nous n’avons pas associé de noms aux lignes du tableau de données, il pourrait être préférable d’afficher le nom seulement des variables :
biplot(acp, type = c("text","point"))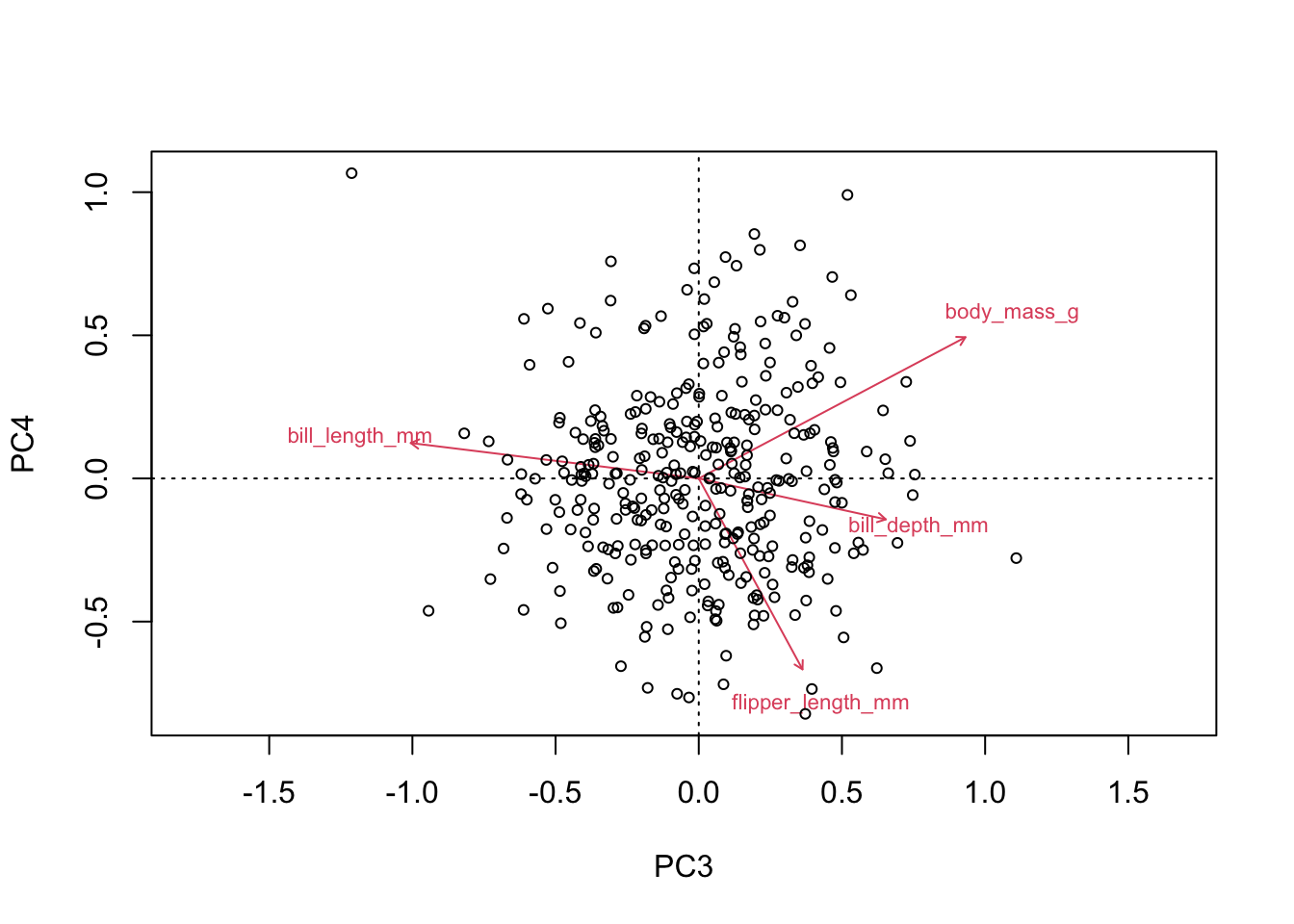
On constate donc dans ce graphique exactement la même chose :
- Un premier axe (gauche à droite) décrivant la grosseur des oiseaux.
- Un deuxième axe (de haut en bas) décrivant la grosseur des becs. Remarquez que sur cet axe, les grandes valeurs sont vers le bas.
La conclusion de notre analyse est donc que les 4 variables décrivants nos manchots peuvent être essentiellement remplacées par 2 variables seulement : une décrivant la grosseur de l’oiseaux et l’autre la grosseur du bec. Si on utilise ces deux axes plutôt que les 4 variables originales, on perd à peine 12% d’information (100%-88%).
Une façon de bien comprendre un graphique d’ACP est de l’analyser quadrant par quadrant :
- En haut à gauche, on a des petits oiseaux avec des petits becs
- En haut à droite, de grands oiseaux avec des petits becs
- En bas à gauche de petits oiseaux avec de grands becs et
- En bas à droite, de grands oiseaux avec de grands becs.
Remarquez que les variables associées au bec sont presque parfaitement en diagonale entre les deux premiers axes. Si on rapporte par exemple la position de la pointe de la flèche de bill_length_mm sur l’axe horizontal, elle arrive à peine derrière les deux autres variables. Il aurait donc aussi été légitime de décrire l’axe 1 comme :
Oiseaux lourds, avec de grandes ailes et de longs becs minces à droite et oiseaux légers, avec de petites ailes, et des becs courts et épais à gauche.
L’interprétation de l’ACP n’est pas tranchée au couteau. Il faut utiliser votre connaissances du système à l’étude et votre jugement pour faire le meilleur usage des résultats de l’analyse.
Remarquez qu’avec la fonction biplot, on peut aussi choisir de voir d’autres axes que les deux premiers. On pourrait par exemple regarder comme ceci le troisième avec le quatrième :
biplot(acp, choices = c(3,4), type = c("text","point"))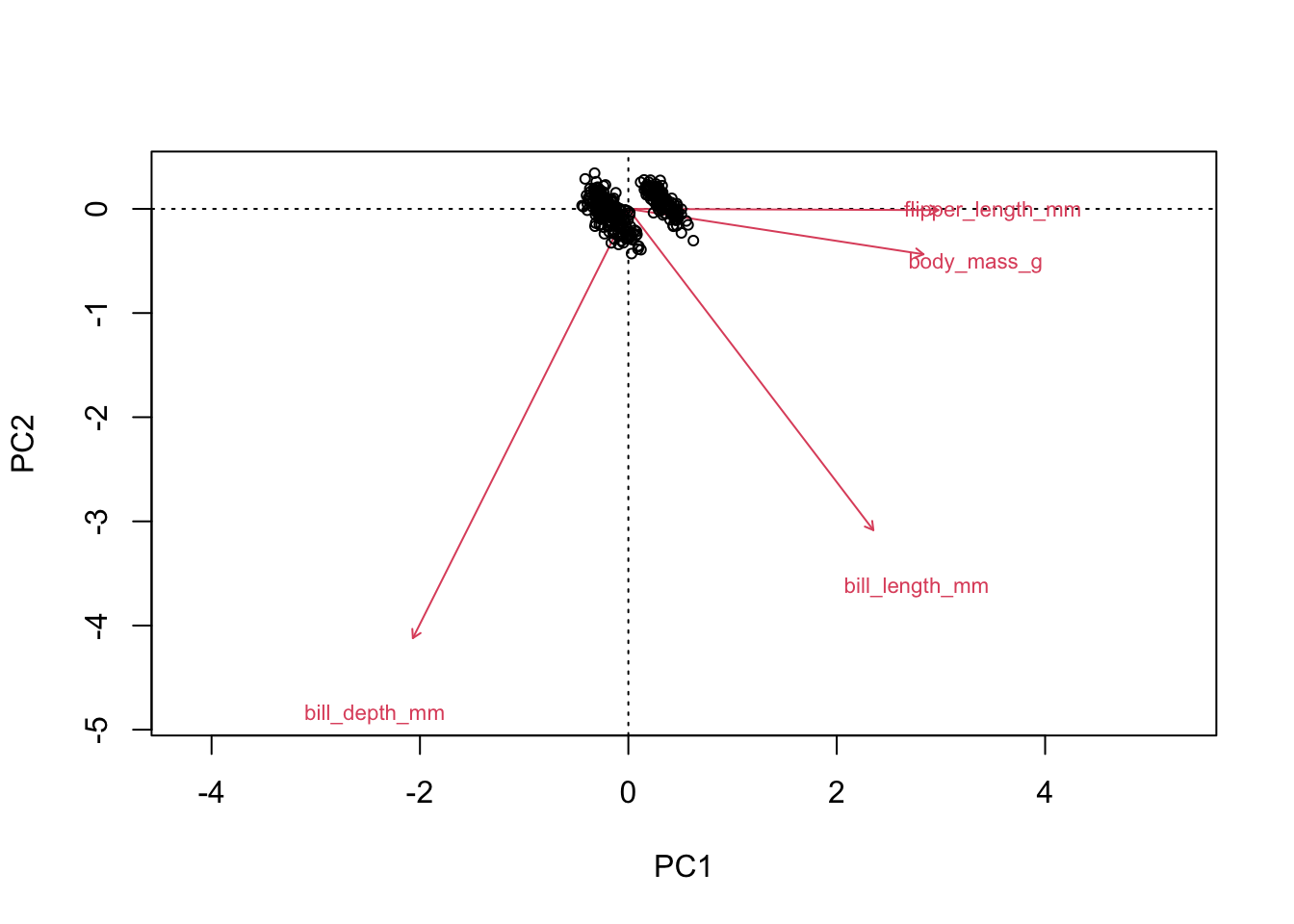
Par défaut, la fonction biplot utilise le cadrage de type II, permettant d’interpréter les variables. Pour utiliser le cadrage de type I, il faut ajouter l’argument scaling = "sites", comme ceci :
biplot(acp,scaling = "sites", type = c("text","point"))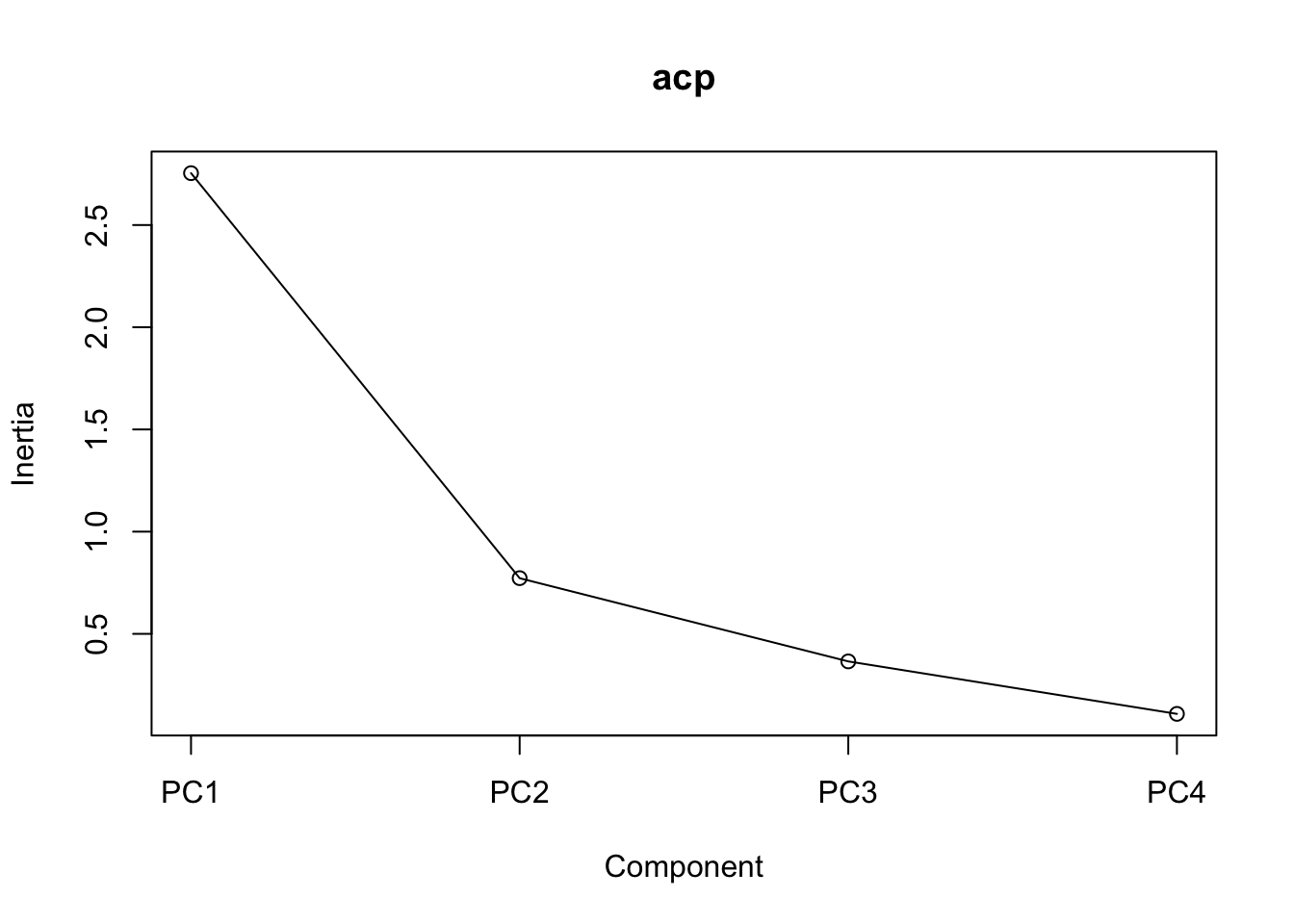
Nous avons vu dans les étapes précédentes comment retrouver chacune des données nécessaires pour utiliser les règles permettant de nous aider à savoir combien d’axes interpréter dans une ACP (Proportion explained, Cumulative proportion, etc). Il existe aussi une fonction nommée screeplot, permettant de visualiser facilement le diagramme en éboulis :
screeplot(acp, type = "lines")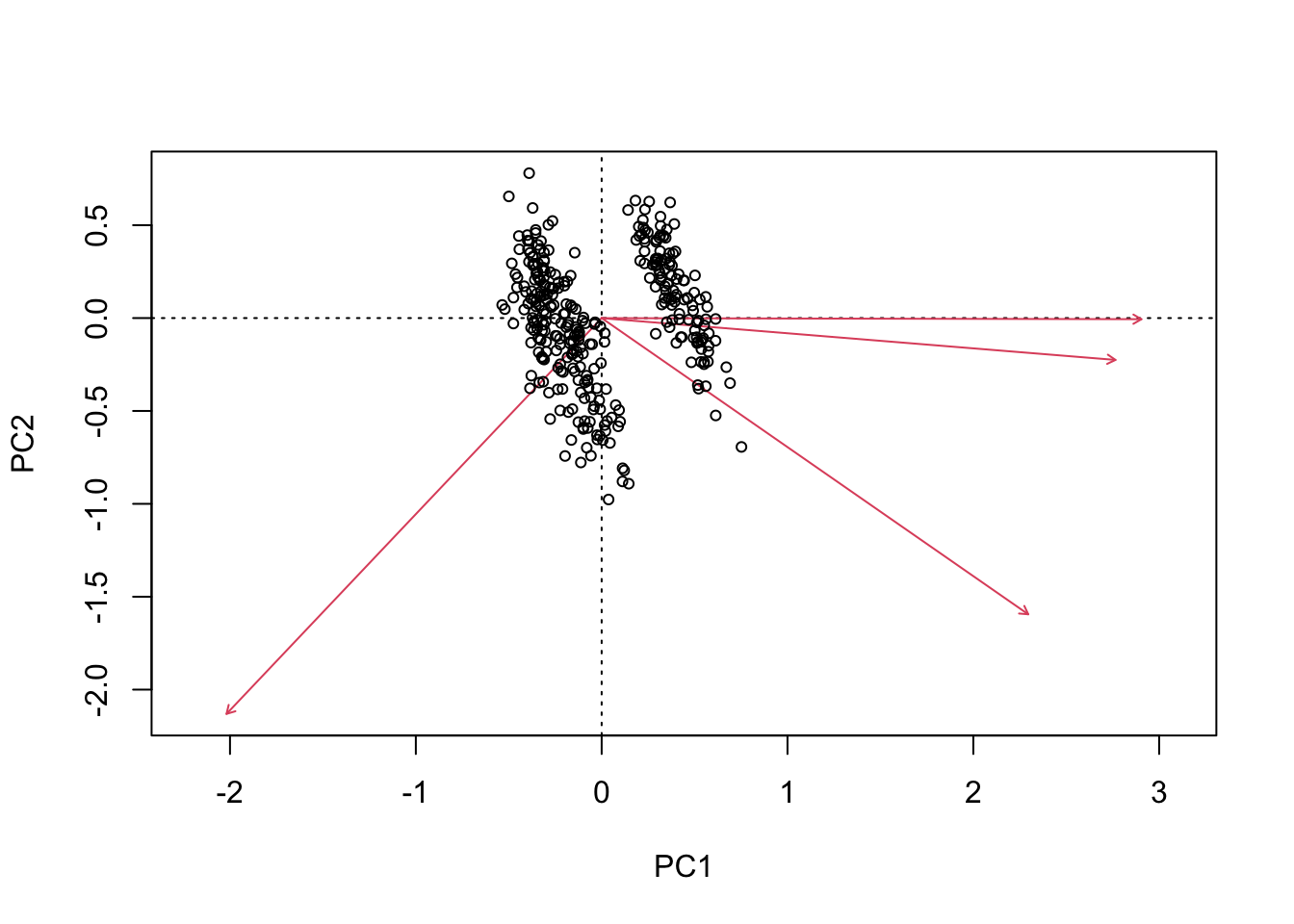
Basé sur ce graphique, le point d’inflexion semble survenir au 2e axe. J’aurais donc probablement interprété deux axes.
23.8 Exercice : L’analyse en composantes principales
Comme exercice sur l’ACP, nous travaillerons sur une petite base de données que j’ai construite à partir de données d’environnement Canada concernant la météo moyenne de certaines villes du Canada et d’autres partout dans le monde1.
Après avoir chargé le fichier, assurez-vous d’éliminer la colonne Neige.cm. Puisqu’elle contient beaucoup d’observations manquantes, nous ne l’utiliserons pas dans cet exercice.
Notre base de données contiendra donc pour chaque ville 6 variables :
- Precip.mm : La quantité de précipitations dans une année
- Jours.Precip : Le nombre de jours dans une année où il y a au moins une goutte de précipitations
- T.Max.Moy : La moyenne des températures quotidiennes
- T.Moy.Mois.Froid : La température moyenne du mois le plus froid
- T.Moy.Mois.Chaud : La température moyenne du mois le plus chaud
Pour cet exercice, assumez que j’ai déjà fait la vérification pour vous, et que les données sont suffisamment normales et les relations suffisamment linéaires pour donner de bons résultats avec l’ACP.
Donc, à partir des ces données :
- Calculez une ACP à partir de la matrice de corrélation,
- À partir des eigenvectors, déterminez quelles variables sont les plus associées à l’axe 1 et à l’axe 2,
- Visualisez les deux premiers axes de cette ordination à l’aide d’un graphique,
- Déterminez avec l’aide d’un diagramme en éboulis (screeplot) combien d’axes pourraient être interprétables dans cette analyse.
- Comment ce résultat se compare-t-il avec le nombre d’axes qui auraient été retenus si on avait interprété tous les axes ayant un eigenvalue > 1.
- Quelle interprétation donnez-vous aux axes 1 et 2 de l’ACP. Que représentent-ils, dans vos propres mots?
23.9 Contenu optionnel : Personnaliser un graphique d’ACP avec ggplot2
Il existe quelques options permettant de personnaliser les graphiques de la fonction biplot de vegan, mais les options sont relativement limitées. Si jamais vous voulez personnaliser vos graphiques d’ACP entièrement à votre goût, il est aussi possible de le recréer avec ggplot2. Nous aurons besoin, pour ce faire, d’extraire les coordonnées de nos observations et de nos variables originales dans le nouveau système d’axes de l’ACP.
Ce travail se fait en 3 étapes. D’abord, on doit refaire la fonction biplot, mais récupérer le résultat dans un objet. Ici on l’appellera x pour la simplicité.
x <- biplot(acp)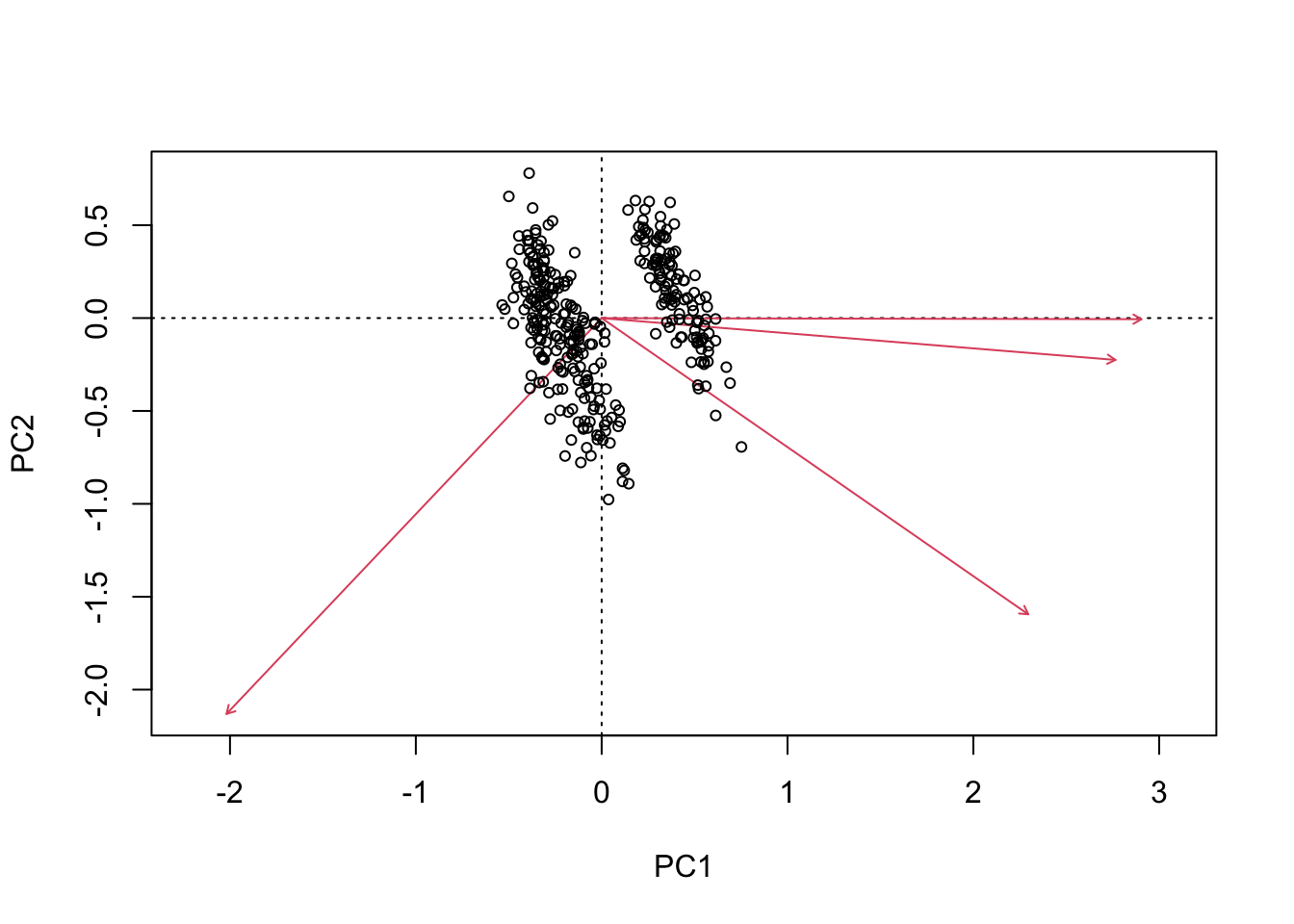
On extrait ensuite de cet objet les nouvelles coordonnées des variables :
variables <- x$species |>
as.data.frame() |>
rownames_to_column("variable")Et puis celles des observations :
observations <- x$sites |>
as.data.frame()Une fois ces étapes effectuées, ne reste plus qu’à les utiliser avec ggplot2 pour construire notre graphique d’ACP à notre goût. La clé pour y arriver est de savoir que l’argument data est aussi disponible dans une couche graphique, pour qu’elle utilise des données provenant d’un second tableau. Voici le graphique le plus simple que l’on aurait pu faire :
observations |>
ggplot(aes(x = PC1, y = PC2)) +
geom_point() +
geom_text(
data = variables,
aes(label = variable)
)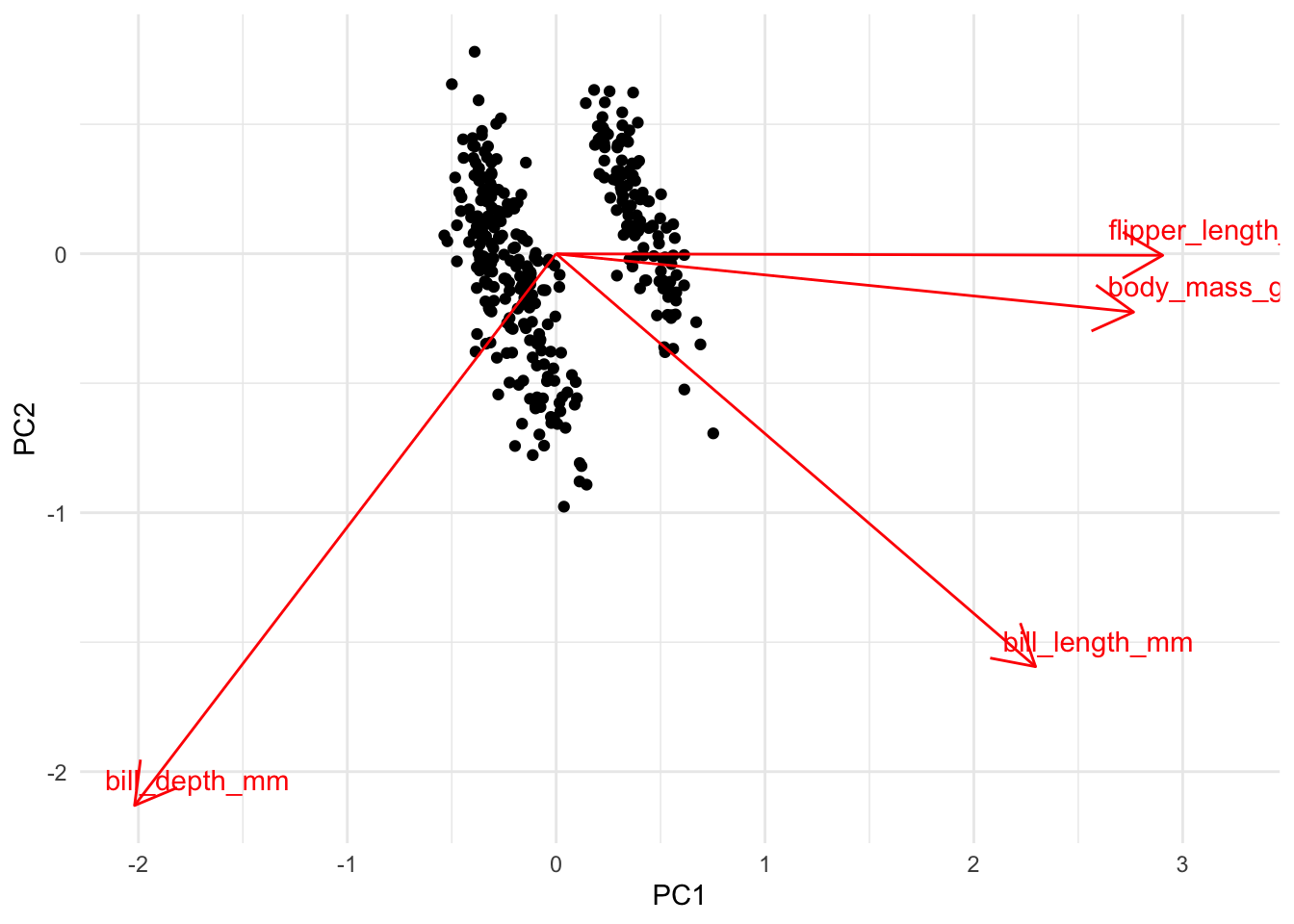
Avec légèrement plus de travail, il est aussi possible d’ajouter les flèches. Remarquez que, pour cet exemple, je décale aussi légèrement les étiquettes pour ne pas qu’elles se superposent avec les pointes des flèches :
observations |>
ggplot(aes(x = PC1, y = PC2)) +
geom_point() +
geom_text(data = variables, aes(label = variable, x = PC1+0.3, y = PC2+0.1), color = "red") +
geom_segment(
data = variables, aes(xend = PC1, yend = PC2, x=0,y=0),
arrow = arrow(),
color = "red"
) +
theme_minimal()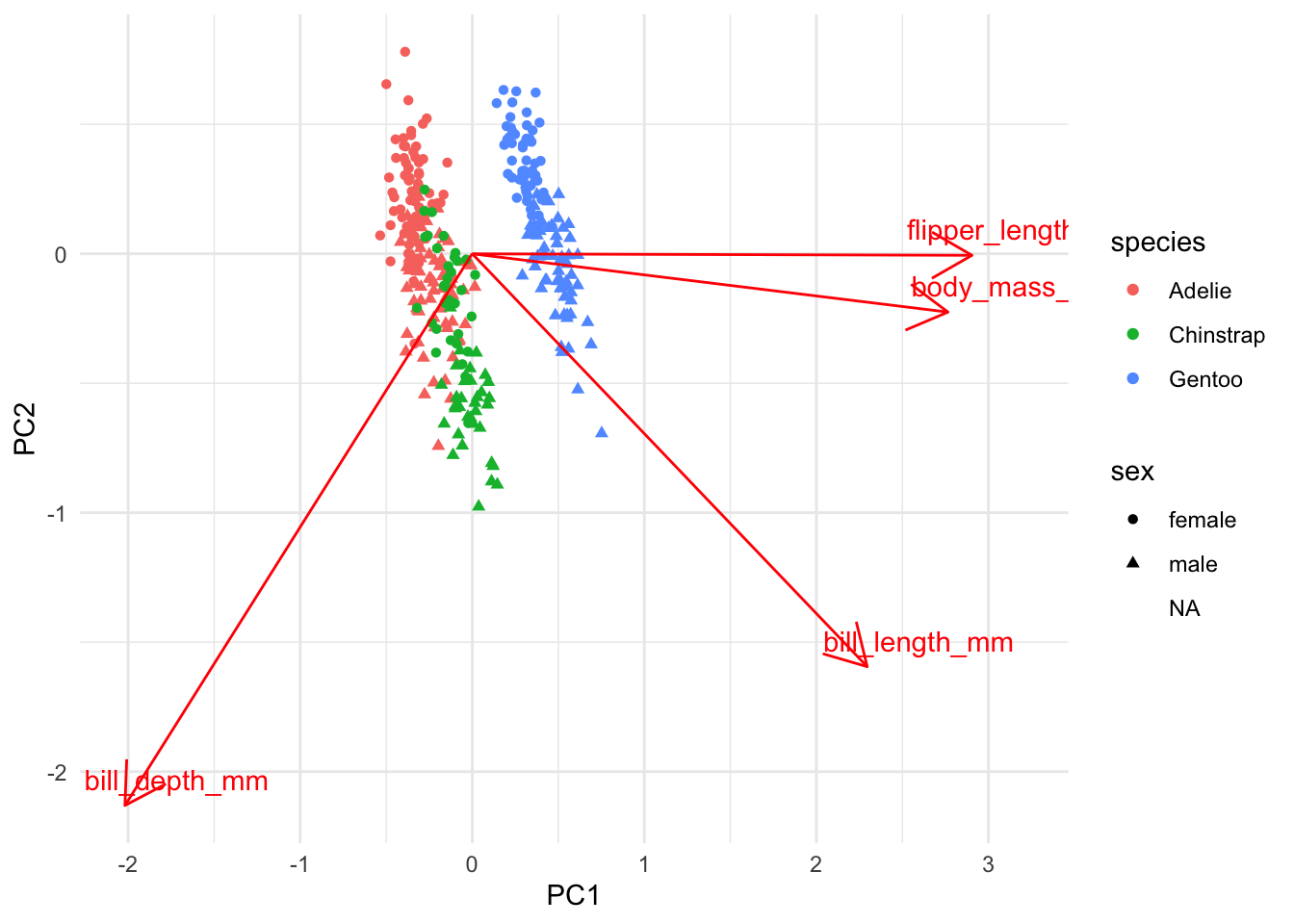
Enfin, comme discuté plus haut, il peut être intéressant d’ajouter de l’information supplémentaire au graphique, par exemple en colorant les points selon l’espèce et en changeant leur forme selon le sexe du manchot. Pour se faire, il faut connecter le tableau d’informations complémentaires au tableau d’observations avant de tracer le graphique :
observations |>
bind_cols(infos_complementaires) |>
ggplot(aes(x = PC1, y = PC2)) +
geom_point(aes(color = species, shape = sex)) +
geom_text(data = variables, aes(label = variable, x = PC1+0.3, y = PC2+0.1), color = "red") +
geom_segment(
data = variables, aes(xend = PC1, yend = PC2, x=0,y=0),
arrow = arrow(),
color = "red"
) +
theme_minimal()Warning: Removed 9 rows containing missing values or values
outside the scale range (`geom_point()`).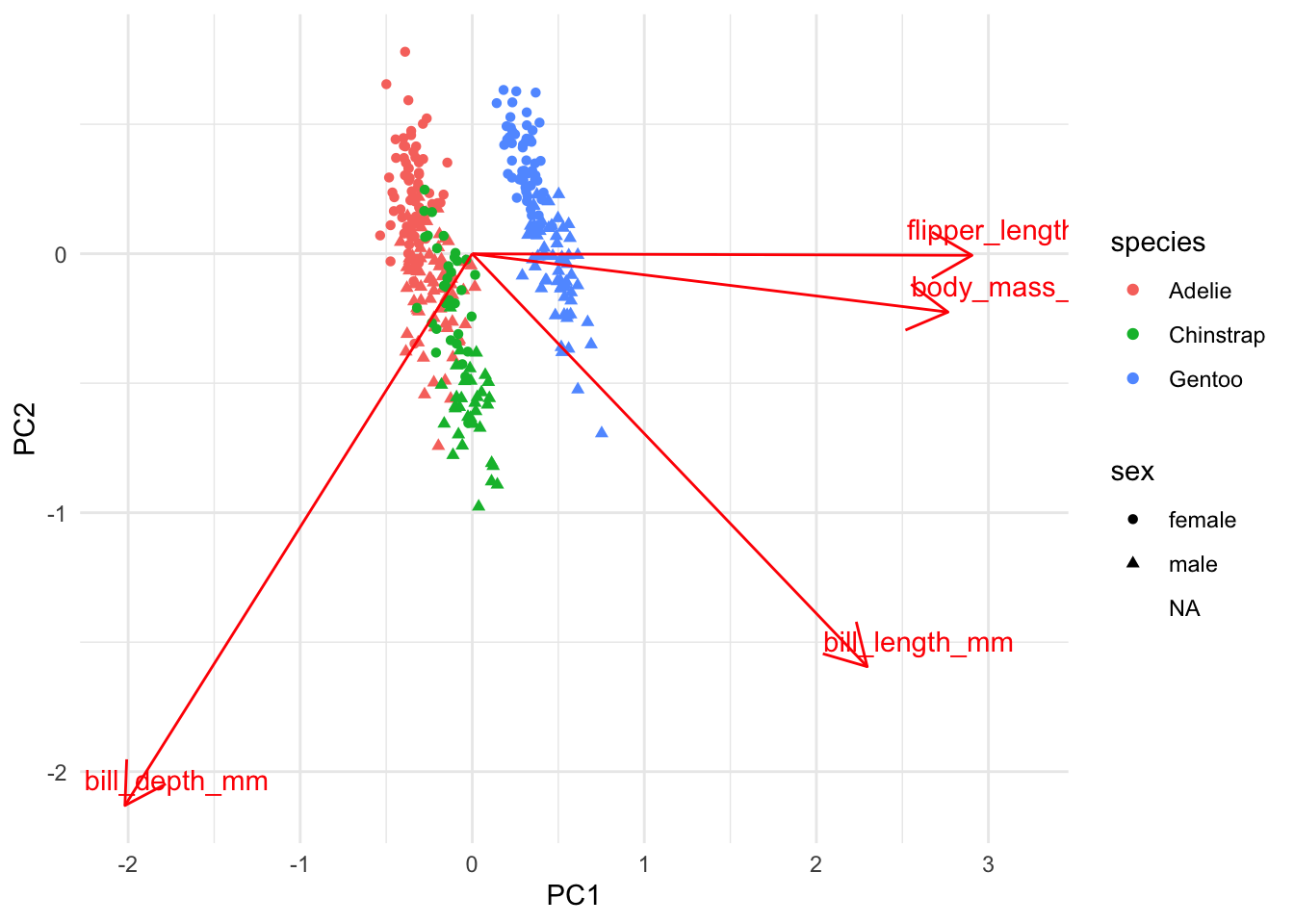
Dans ce graphique, on peut donc constater qu’en général, les manchots Gentoo sont plus grands que les deux autres espèces (plus à droite sur le 1er axe), qui ne se distinguent pas beaucoup sur les deux axes illustrés. Leurs différences de niches écologiques doit se situer dans d’autres variables que nous n’avons pas mesurées.
On peut aussi constater que les mâles ont en général des becs plus gros que les femelles (plus en bas sur l’axe 2), et ce, peu importe l’espèce.
Notez cependant que le but de l’ACP n’est pas de trouver des groupes comme tel. Le but de l’ACP est de résumer la variabilité dans un nombre réduit d’axes. Si on veut déterminer si il existe des groupes dans nos données ou non et comment les séparer, il faut consulter les techniques du Chapitre 26.
23.10 Un exemple concret
Voici, pour terminer ce chapitre, un exemple concret d’ACP que j’ai effectuée pour mon projet de maîtrise. Dans mes travaux terrain, nous avions visité une 50aine de peuplements forestiers du Parc National de la Mauricie. Pour chacun, nous avions noté (entre autres), la densité d’arbres, la densité de gaules, le couvert latéral, le diamètre des arbres (DHP) et une mesure de stratification de la forêt (diversité de hauteur de feuillage). Une fois la saison de terrain terminée, une des premières choses que j’ai fait était de faire une ACP pour voir à quoi ressemblaient mes données. Notez que comme ces variables sont à des échelles très différentes, j’ai dû calculer mon ACP sur la matrice de corrélation.
Voici le graphique de mes résultats :
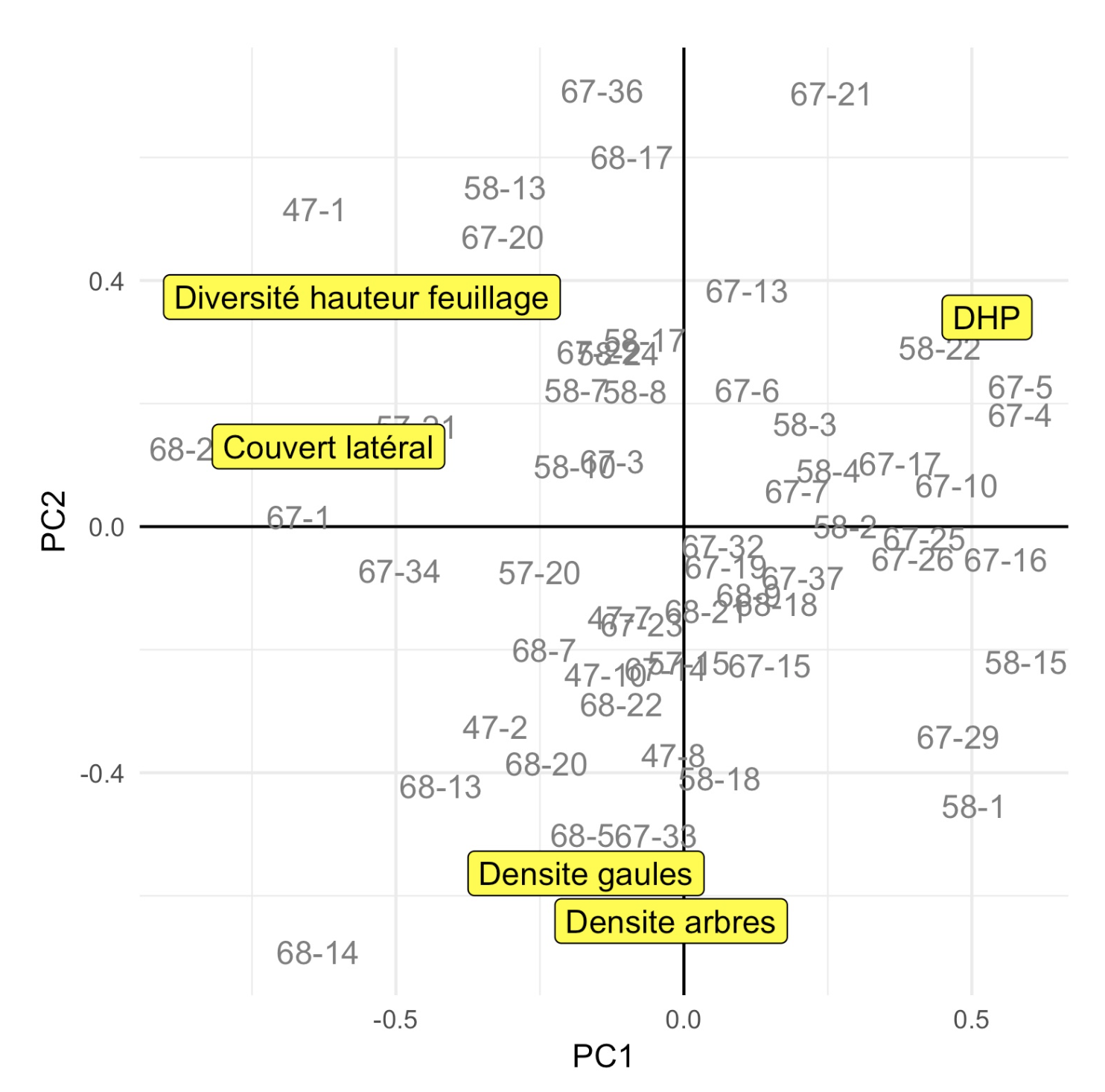
Moi et mon directeur étions bien contents de ce graphique, puisque les axes fournis étaient facilement interprétables et nous permettaient de bien comprendre/décrire nos peuplements.
Le premier axe de l’ACP, formé d’un côté par le DHP et de l’autre le couvert latéral et la diversité de hauteur nous informait facilement sur l’ouverture du sous-bois. Les sites à droite sont formés de grands arbres, entre lesquels il n’y a pas grand chose. On y marche facilement. Les sites à gauche sont formés de petits arbres, avec beaucoup de branches basses et d’arbustes en sous-bois. Ce sont des sites où il est difficile de circuler, mais facile de se cacher.
Le deuxième axe, quant à lui, nous informait clairement de la quantité de tiges que l’on pouvait trouver dans un site. Il était formé essentiellement des deux variables de densité d’arbres et de densités de gaules.
L’ACP nous informait que ces deux gradients étaient relativement indépendants, et que l’on pourrait donc en faire des analyses combinées sans problèmes.
23.5 Comment faire l’interprétation?
Il existe deux façons de présenter les résultats de l’ACP et d’en faire l’interprétation. On peut soit regarder le tableau des eigenvectors ou soit regarder le graphique d’ordination (biplot). Les deux stratégies nous apportent exactement la même information.
Nous analyserons les données présentées au Chapitre 22, où nous avions capturé 5 poissons, sur lesquels nous avions mesuré la longueur, le poids et noté la profondeur de la capture. Nous avons appliqué une ACP basée sur la matrice de corrélation, puisque nos mesures étaient à des échelles différentes. Observons d’abord le tableau des eigenvalues, afin de se donner une idée d’où arrêter notre interprétation, en se basant sur le fait que l’on veut interpréter tous les axes jusqu’à 95 % de la variance :
Dans ce cas-ci, nous interpréterons donc les deux premiers axes. Remarquez que ce tableau va de gauche à droite plutôt que de haut en bas comme le précédent, mais il contient exactement la même information.
Maintenant, observons le tableau des eigenvectors :
Première chose à remarquer : dans ce tableau, on ne parle PAS de fraction expliquée contrairement au tableau précédent. Il s’agit de coefficients, un peu comme les paramètres d’une régression, qui peuvent donc avoir des valeurs négatives. Chacun des nombres nous indique à quel point une des variables originale (par exemple longueur) est associée à une composante principale (par exemple l’axe 1). On voit, entre autres, que l’axe 1 est fortement associé aux trois variables (en valeur absolue). L’axe 2 quant à lui est plus associé (en valeur absolue) à la longueur et au poids, et moins à la profondeur.
Pour le sens du coefficient (positif ou négatif), il n’a par lui-même pas d’interprétation. On aurait pu inverser l’ensemble des signes (i.e. que chaque négatif soit un positif et chaque positif soit un négatif) et avoir exactement la même interprétation. Ce qu’il est surtout important d’observer est si des variables sont du même signe ou non sur un axe. Si elles ont le même signe, elles sont corrélées (ou associées) positivement. Si elles ont des signes différents, elles sont associés négativement (i.e. quand l’une augmente, l’autre diminue). Par exemple, pour l’axe 1, la profondeur et la longueur sont associées positivement (elles ont le même signe), alors que ces deux variables sont associées négativement au poids (qui a un signe différent).
Voyons maintenant comment ces mêmes résultats se traduisent de manière visuelle :
On y constate la même information, soit que la variable poids est seule de son côté de l’axe 1 (à droite) et les variables longueur et profondeur sont associées ensemble de l’autre côté (à gauche). On voit aussi que sur le deuxième axe, poids et longueur sont associées d’un côté (en bas) et profondeur de l’autre (en haut).
Notez que pour entrer à la fois les variables et les observations dans un même graphique, un cadrage (mise à l’échelle) doit être effectué. Cette opération peut être effectuée de plusieurs façons, entre autres :
Donc, si l’intérêt est de comparer les observations, il faut utiliser le cadrage de type I, si l’intérêt est les variables (flèches), utiliser le type II. Par défaut, la majorité des fonctions d’ACP utilisent le cadrage de type II, permettant d’interpréter les variables.
Et maintenant la partie la plus difficile, donner un sens aux axes de l’ACP. Notez d’abord qu’il n’y a aucun test statistique qui peut vous venir en aide ici. Seul votre jugement de biologiste et votre connaissance du système à l’étude pourrons vous aider.
Donc, que représentent les axes? L’axe 1 n’est pas simple à interpréter. Il semble nous indiquer que plus les poissons sont capturés en profondeur, plus ces derniers sont longs, mais minces. Si ce n’était pas des données fictives, nous aurions probablement pu conclure qu’il s’agit d’une sorte de compromis fonctionnel, où il est plus avantageux d’être mince que gros en profondeur. Remarquez cependant que l’ACP ne fournit pas de lien de cause à effet. On ne sait pas si la profondeur cause la longueur ou l’inverse. L’axe 2 est plus facilement interprétable. Puisque le poids et la longueur y sont associées positivement et que la profondeur y est moins associée, on peut probablement y voir un gradient de taille de poissons. D’un côté de l’axe (en bas), les poissons sont longs et lourds, de l’autre côté, petits et légers.
On peut donc dire que les deux gradients principaux dans notre jeu de données étaient premièrement un compromis fonctionnel selon la profondeur et un deuxièmement un gradient de taille. On pourrait aussi affirmer qu’à eux seuls, ces deux gradients expliquent 99 % de la variabilité de notre jeu de données.
Dans la vraie vie, il est rarement possible de donner un sens aux axes après le 2e ou le 3e. Ils deviennent trop abstraits pour notre pauvre cerveau humain!