pnorm(14, mean = 12, sd = 1)[1] 0.977249911 Les lois de probabilité
11.1 L’utilité des lois de probabilité
La première chose qui vous viendra probablement à l’esprit est : c’est quoi une loi de probabilité et à quoi ça peut bien servir? Une loi de probabilité est un outil statistique, une représentation de la réalité. Nous avons vu au Chapitre 3 que l’on peut visualiser la variabilité d’une variable à l’aide d’un histogramme de fréquences. Les lois de probabilité permettent de décrire certaines formes classiques d’histogrammes. Pour ne pas avoir à dire : beaucoup d’observations au milieu, pas beaucoup dans les bouts, les côtés symétriques avec un seul mode. Il peut être avantageux d’avoir un terme qui définit une telle forme, p. ex. ici la distribution normale.
De même, puisqu’une loi de probabilité est définie par des fonctions mathématiques (les fonctions de densité et de répartition), il est possible de l’utiliser pour effectuer des calculs de probabilité et de faire des inférences à partir de certains de ses paramètres.
D’un point de vue sémantique, les lois de probabilités définissent des distributions de fréquences. La loi normale définit la distribution normale, la loi de Poisson définit la distribution de Poisson, etc. On peut donc souvent utiliser un terme ou l’autre (loi ou distribution), puisqu’ils font référence au même concept.
11.2 Structure de la loi normale
La loi de probabilité la plus utilisée en biologie est sans aucun doute la loi normale. Cette dernière suit la forme classique d’une courbe en cloche (bell curve), parfois nommée aussi la loi de Gauss.
Comme suggéré précédemment, la loi normale se caractérise principalement par la présence d’un seul mode, et d’une distribution symétrique des probabilités de chaque côté. Elle est définie par deux paramètres, soit sa moyenne et sa variance (ou son écart type, dépendant des définitions).
Elle survient fréquemment dans la nature pour décrire la variabilité des phénomènes naturels comme la taille et le poids de la plupart des espèces, la pression artérielle, le Q.I., etc. Lorsqu’un phénomène naturel peut se définir comme la somme de plusieurs événements aléatoires, la forme finale de la distribution risque fort de correspondre à la loi normale. La taille et le poids sont, entre autres, dans cette catégorie car la taille d’un animal adulte dépend généralement de l’activation ou non d’une série de gènes définissant sa croissance.
Il est important de comprendre que ce ne sont pas tous les phénomènes naturels qui produiront des distributions normales. Certains autres, p. ex. les tremblements de terre ou les décès liés à la guerre auront plutôt tendance à présenter une longue queue d’un côté, parce que certains événements sont beaucoup plus rares alors que d’autres sont très communs. Il survient des dizaines de milliers de tremblements de terre de faible magnitude par année et seulement quelques-uns sont plus importants.
Dans la distribution normale, les probabilités de chaque côté de la moyenne sont égales. Si la moyenne du poids des bruants suit une loi normale avec une moyenne de 12 g, il est aussi probable de trouver un bruant de 10 g qu’un bruant de 14 g.
11.3 La règle du 68-95-99,7
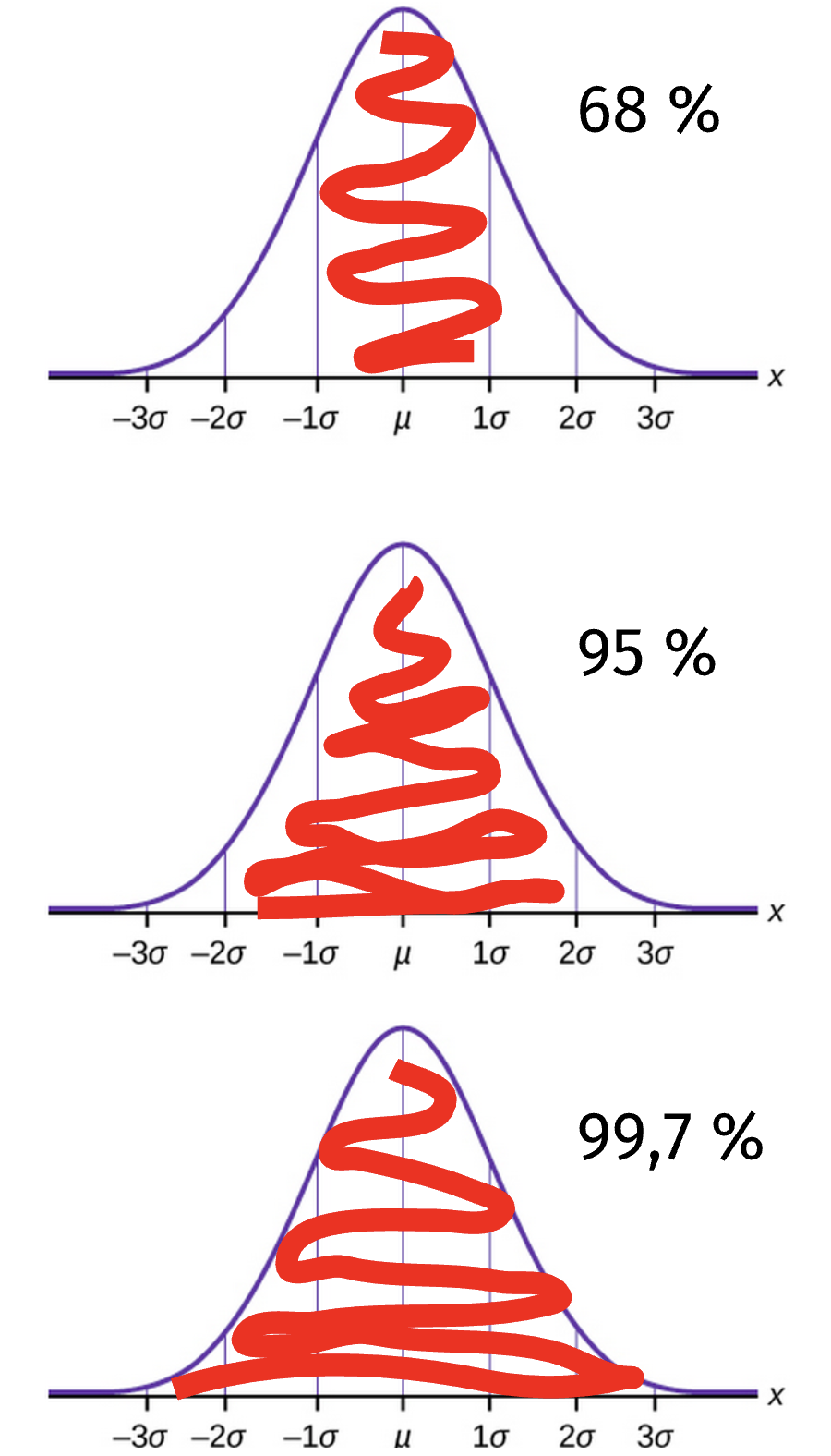
Dans la loi normale, la densité de distribution de probabilités autour de la moyenne est toujours organisée de la même façon. Autour de la moyenne, nous trouverons 68 % des observations à l’intérieur d’un écart-type, 95 % des observations à l’intérieur de deux écarts-types et 99,7 % à l’intérieur de trois écarts-types de la moyenne. On nomme ce phénomène la loi du 68-95-99,7.
Connaissant la moyenne et l’écart-type d’un phénomène répondant à la loi normale, il est facile d’évaluer rapidement certaines probabilités en se basant sur cette règle. Si l’on retourne à nos bruants pesant en moyenne 12 g et que l’on sait que l’écart-type de cette distribution est de 1 g, on peut affirmer que 95 % des bruants que nous observerons pèseront entre 10 et 14 g. On peut aussi utiliser cette règle dans l’autre sens. Pour la même population de bruants, si l’on trouve un individu pesant 15 g, on peut affirmer qu’il s’agit d’un phénomène rare, puisque seulement 0,3 % (100 % - 99,7 %) des bruants auront un poids aussi extrême.
Notez qu’il s’agit d’une règle pour faire des calculs “au pif”, rapidement sans avoir recours à un ordinateur. Les valeurs calculées seront approximatives, mais suffisantes pour valider un calcul ou avoir une idée de grandeur d’un chiffre en lisant un rapport, par exemple.
11.4 Labo : Calculer des probabilités basées sur la loi normale
Dans le logiciel R, il est possible d’effectuer rapidement des calculs basés sur les probabilités de la distribution normale. Il existe deux fonctions différentes pour le faire, une lorsque l’on recherche la probabilité associée à une valeur (pnorm; Probability NORMal) et une autre lorsque l’on cherche la valeur associée à une probabilité (qnorm; Quantile NORMal).
P ex. pour déterminer la probabilité d’observer un bruant de 14 g dans une population dont la moyenne est 12 et l’écart-type est 1, nous utiliserons le code suivant :
R nous retourne la valeur 0,977. En se basant sur la loi du 68-95-99,7 expliquée ci-haut, on se serait attendu à obtenir 0,95. Que s’est-il passé?
Ce qu’il faut comprendre est que la fonction pnorm calcule les probabilités de façon cumulative à partir de zéro, de gauche à droite. Elle nous informe que notre bruant de 14 g est plus grand que 97,7 % des bruants. Il y a un autre 2,3 % de bruant qui se trouvent à être deux écarts-types plus petits que la moyenne. On peut le voir en faisant :
pnorm(10, mean = 12, sd = 1)[1] 0.02275013R nous retourne 0,023. Il y a donc 2,3 % de bruants à deux écarts-types sous la moyenne et un autre 2,3 % au-dessus de la moyenne. Il y a donc, effectivement 95,4 % des bruants à l’intérieur de 2 écarts-types de la moyenne.
Notez que nous arrivons à 95,4 %, le vraie proportion de données à deux écarts-types de la moyenne, plutôt que 95 %, qui est un chiffre facile à retenir pour faire des choses “au pif”.
Le point important à comprendre ici est que, lorsque l’on discute de probabilités issues d’une distribution, il est important de spécifier si notre probabilité est bilatérale ou unilatérale. Une probabilité unilatérale est entièrement d’un côté de la distribution. On peut p. ex. dire que 95 % des bruants sont plus petits que 13,6 g. Au contraire, une probabilité bilatérale est partagée de façon égale de chaque côté. On peut p. ex. dire que 95 % des bruants ont un poids entre 10 et 14 g. On aurait alors séparé le 5 % également, 2,5 % de chaque côté de la distribution.
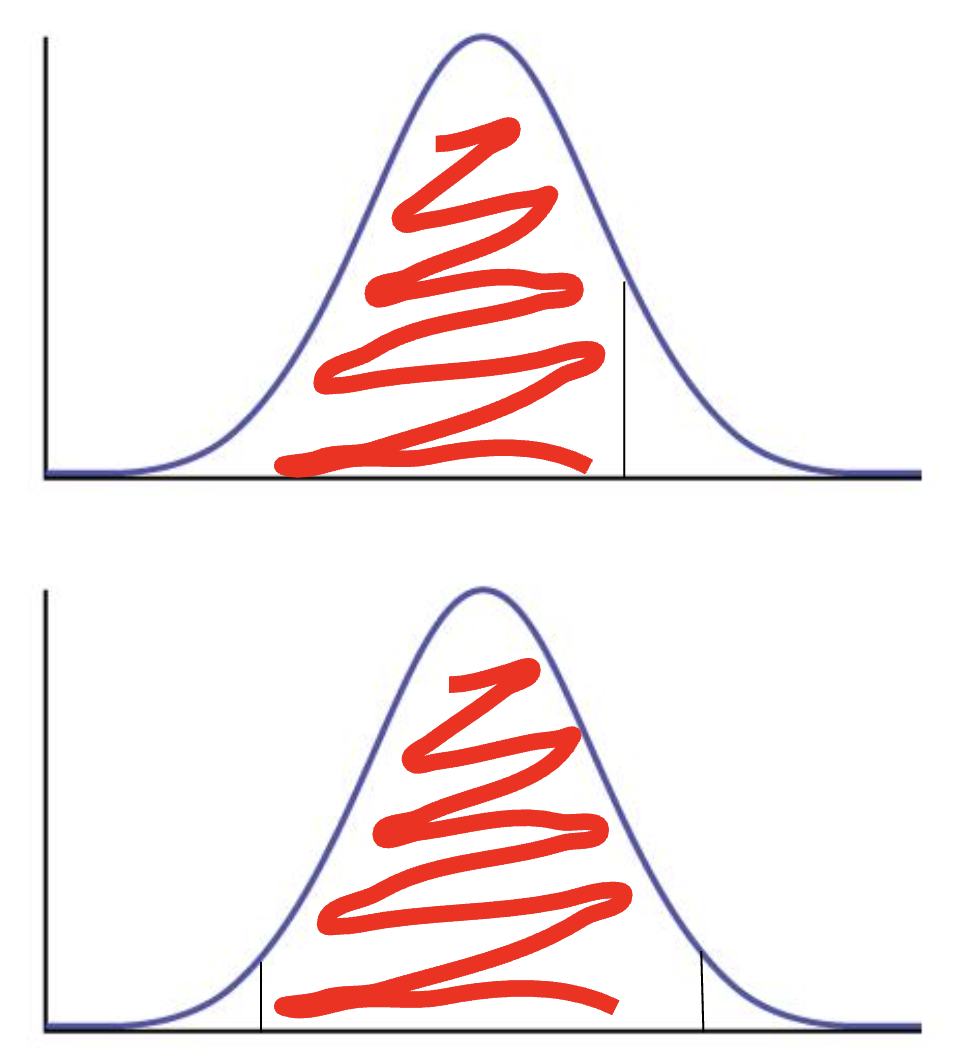
Comme mentionné précédemment, on peut utiliser la fonction qnorm pour savoir à quelle valeur correspond une probabilité. Dans notre même distribution de bruants (moyenne 12, écart-type 1), si l’on veut savoir à quoi correspondrait un bruant plus grand que 99 % des autres individus, on peut utiliser le code suivant :
qnorm(0.99,mean = 12, sd = 1)[1] 14.32635Ce qui nous donne 14,3 g.
11.5 Le théorème central limite
Ce n’est pas un hasard si les phénomènes naturels pouvant être décrits par l’addition de la probabilité d’événements indépendants peuvent être décrits par une loi normale. Il existe un principe statistique sous-jacent à ce phénomène, nommé le théorème central limite. Le théorème central limite stipule que des échantillons formés par l’addition d’au moins une vingtaine d’observations aléatoires produiront ensemble une distribution normale, sous certaines conditions1. Ce qui est remarquable avec ce phénomène est qu’il est vrai peu importe la forme de la distribution dans laquelle les observations aléatoires sont pigées pour former les échantillons. Même pour un tirage à pile ou face ou un lancé de dé. Si chaque échantillon est formé par la somme de 20 lancers à pile ou face, la distribution de ces échantillons (i.e. si on recommençait nos 20 lancers plusieurs fois) formera toujours une distribution normale.
Notez que le théorème s’applique autant aux moyennes qu’aux additions, puisqu’il s’agit du même principe mathématique.
11.6 Les autres lois
Il existe, évidemment, une série d’autres lois de probabilités que la loi normale. Puisque la majorité des techniques statistiques enseignées dans ce cours exigent que les données suivent une loi normale, nous de verrons ici qu’un bref aperçu du reste des lois.
Une des lois statistiques les plus communes que l’on peut rencontrer dans la vie de tous les jours est sans doute la loi binomiale. Cette loi décrit le nombre de succès obtenus lorsque l’on répète plusieurs événements ayant la même probabilité de succès. Cette loi nécessite aussi deux paramètres, soit le nombre d’essais et la probabilité de succès d’un essai. Contrairement à la loi normale, la loi binomiale définit des données quantitatives discrètes (des dénombrements) plutôt que quantitatives continues.
La façon classique d’illustrer la loi binomiale est avec le lancer d’une pièce de monnaie. Elle permet, par exemple, de savoir quelles seront les probabilités d’obtenir exactement 5 piles, ou plus de 8 piles lorsque l’on lance 10 fois la pièce :
En écologie, cette distribution se rencontrera souvent lorsque l’on veut étudier le nombre de graines qui germineront, le nombre de poissons qui réussiront à franchir un obstacle, etc.
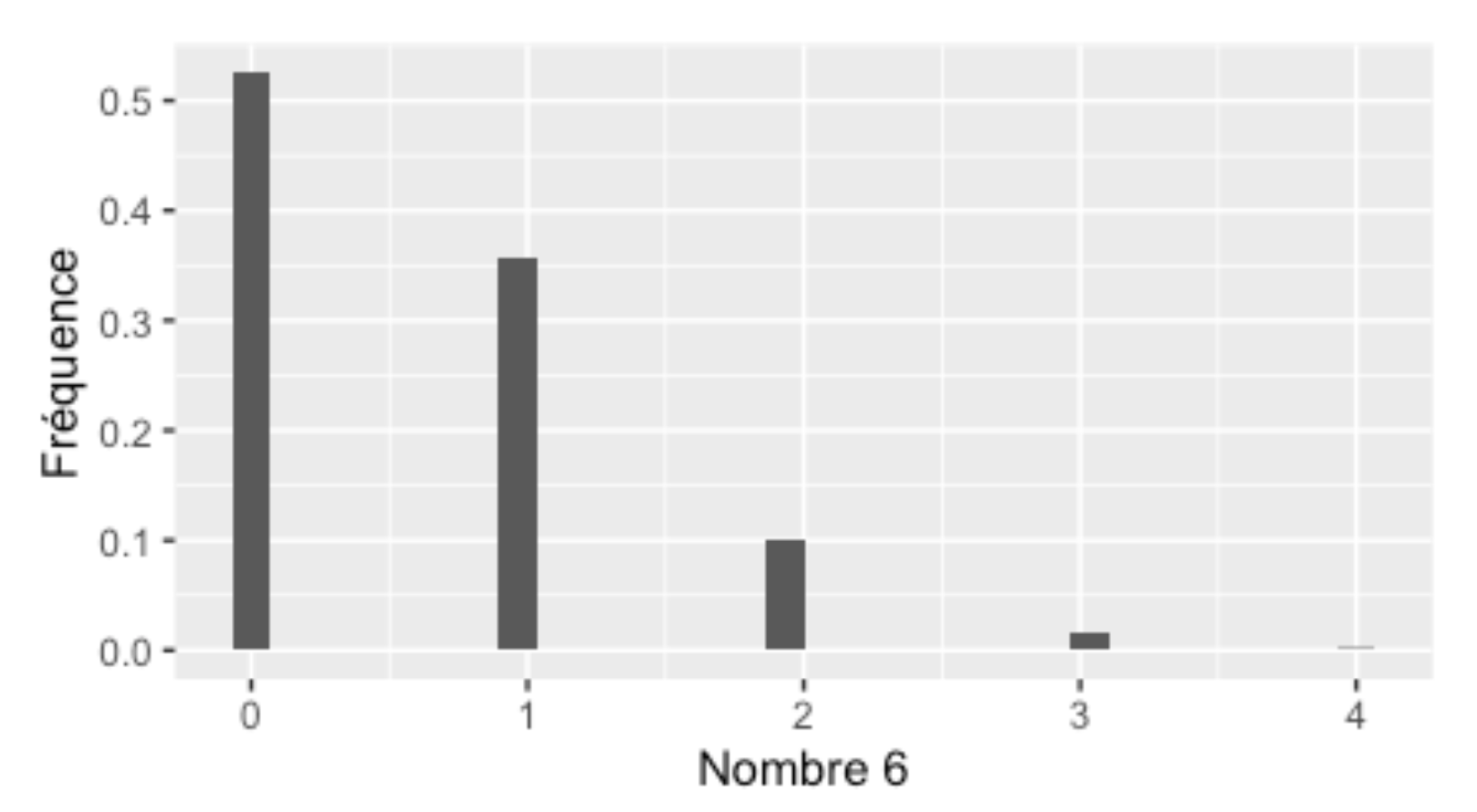
Contrairement à la loi normale, la loi binomiale ne sera pas toujours symétrique. Lorsque les probabilités de succès sont faibles, la distribution viendra s’appuyer à gauche sur la valeur zéro. P. ex. si l’on veut lancer un dé 5 fois, quel pourrait être le nombre de 6 que nous obtiendrons?
Enfin, la dernière loi dont nous discuterons est la loi de Poisson. Cette dernière décrit la probabilité qu’un certain nombre d’événements se produisent dans un intervalle de temps (ou d’espace) donné. Elle peut servir à décrire le nombre d’espèces qui seront rencontrées dans une parcelle, le nombre de brins d’herbe dans une pelouse, etc. Le truc pour bien la cerner est qu’elle est parfaite pour décrire le nombre de poissons péchés dans une journée. Contrairement à la loi binomiale, on ne sait pas à l’avance combien d’essais seront effectués (i.e. on ne sait pas combien il y a de poissons dans le lac).
La propriété particulière de la loi de Poisson est qu’elle est définie par un seul paramètre, nommé λ (lambda), qui décrit à la fois la moyenne et la variance de la distribution (qui se contrôlent avec deux paramètres différents dans la loi normale).
Voici quelques exemples de distribution de la loi Poisson :
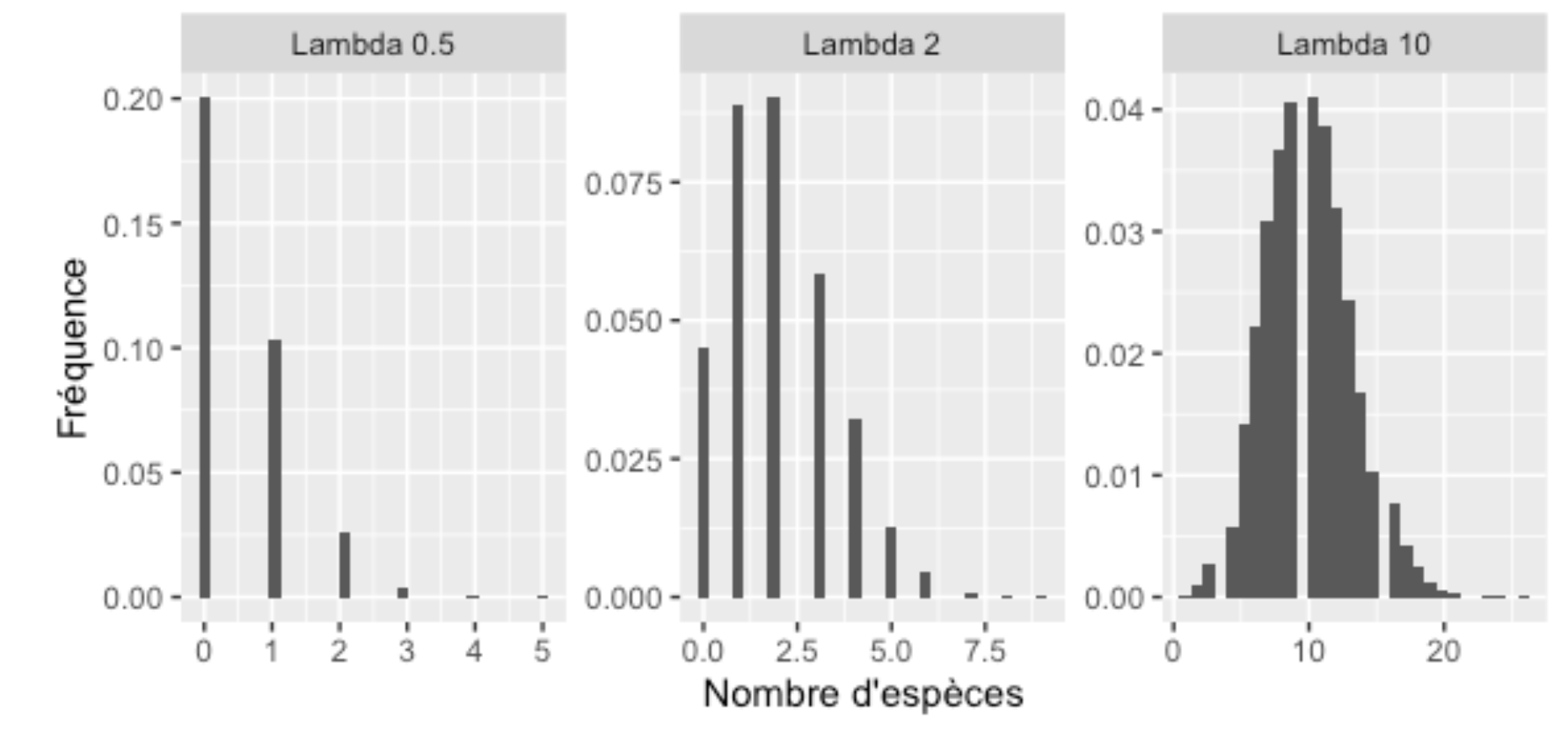
Remarquez que, comme pour la distribution binomiale, la distribution Poisson s’appuie à gauche sur la valeur 0 lorsque la valeur de lambda est faible. Au contraire, lorsque la valeur de lambda est élevée, elle est très semblable à la loi normale.
Cette propriété nous permet d’appliquer parfois des tests statistiques associés à la loi normale à ces deux distributions (Poisson et binomiale). Si leur moyenne est suffisamment élevée, la loi normale en est une excellente approximation, pour autant que l’on accepte que nos résultats puissent nous prédire des choses comme 2,5 espèces ou 3,4 œufs.
11.7 Labo : Calculer les probabilités des lois binomiales et Poisson
Les lois binomiale et Poisson sont aussi implémentées dans R, sous la même forme de deux fonctions que la loi normale. Les fonctions ppois et pbinom nous fournissent des probabilités associées à des valeurs et les fonctions qpois et qbinom nous fournissent des valeurs associées à des probabilités.
P. ex. si l’on veut connaître les chances d’obtenir 5 fois pile ou moins en lançant 10 pièces de monnaie
pbinom(5, size = 10, prob = 0.5)[1] 0.6230469La fonction pbinom attend trois arguments : le nombre de succès pour lequel on attend la probabilité, le nombre d’essais et la probabilité de succès de chacun des essais. On obtient ici 62 %.
Si on voulait savoir l’inverse, p. ex. combien de fois on obtiendrait le côté pile si on était vraiment malchanceux, disons quelque chose qui arriverait 5 % du temps ou moins :
qbinom(0.05, size = 10, prob = 0.5)[1] 2R nous répond que ce niveau de malchance correspondrait à uniquement 2 fois pile sur 10 lancers. Autrement dit, 95 % du temps, on en aurait obtenu plus.
Les fonctions associées à la distribution de Poisson s’utilisent exactement de la même façon. Sachant p. ex. que le lambda (i.e. la moyenne) associé au nombre de chênes dans une parcelle de 10 m2 est de 0,2, le code suivant permettrait de savoir les probabilités d’obtenir un chêne ou moins dans la parcelle :
ppois(1, lambda = 0.2)[1] 0.9824769R nous répond 98,2 %.
Si on veut plutôt savoir à quoi pourrait ressembler une parcelle exceptionnellement riche, que l’on trouverait uniquement 1 % du temps, on utiliserait le code suivant :
qpois(0.99, lambda = 0.2)[1] 2Remarquez qu’ici, puisque l’on veut obtenir le 1% à droite de la distribution et que la fonction calcule dà partir de la gauche, on doit faire 1 - 0,01 = 0,99 pour trouver la probabilité à entrer dans la fonction.
Autrement dit, dans ce contexte, une parcelle contenant deux chênes serait particulièrement exceptionnelle.
11.8 Le concept d’intervalle de confiance
Nous avons vu dans le Chapitre 10 qu’à cause du fait que nous ne possédons que des échantillons et jamais d’information complète sur la population, nous devons avoir sans cesse recours à l’inférence statistique. Ce qui signifie que nous devons sans cesse aussi évaluer notre incertitude sur nos mesures.
Grâce au théorème central limite, les mathématiciens savent non seulement que l’on peut décrire la variation autour de la moyenne d’un échantillon à partir de l’écart-type. Mais ils savent aussi que l’incertitude que cette moyenne échantillonnée soit près de la vraie moyenne de la population peut être quantifiée à l’aide d’une seconde mesure, l’erreur-type, basée sur l’écart-type :
\[ \sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}} \]
Autrement dit, notre incertitude sur notre estimation de la moyenne à partir d’un échantillon (notre inférence) dépend de la variabilité de l’échantillon (qui fait augmenter l’incertitude) et de la taille de l’échantillon (qui fait diminuer l’incertitude).
À partir de l’erreur-type, il est aussi possible de calculer des bornes à l’intérieur desquelles il est probable que la vraie moyenne de la population se trouve, que l’on nomme l’intervalle de confiance.
Ces intervalles ont toujours une notion de certitude associée, p. ex. un intervalle de confiance à 95 % confère beaucoup plus de certitude quand à la position de la moyenne qu’un intervalle à 50 %.
Par contre, inévitablement, l’intervalle de confiance à 95 % sera aussi plus large que celui à 50 %; il doit s’élargir pour qu’on soit vraiment sûr que la moyenne est dedans. Plus il est large, plus il a de chances de contenir la vraie moyenne.
Pour calculer un intervalle de confiance, on se base sur les propriétés de la distribution normale, mais l’on utilise l’erreur-type plutôt que l’écart-type pour effectuer les calculs, puisque nous faisons de l’inférence statistique. Je vous propose trois niveaux de précision différents pour effectuer vos calculs.
D’abord, “au pif”, on peut se baser sur la loi du 68-95-99,7. Sachant que 95 % des données seront dans les bornes de la moyenne ± 2 erreur-type, il est facile de faire le calcul, souvent même mentalement. Si l’on sait que la moyenne de nos données est de 5 et que notre erreur-type est de 1, on sait que l’intervalle de confiance à 95 % autour de cette moyenne est entre 3 et 7, et que celui à 99 % serait entre 2 et 8 (i.e. moyenne ± 3x l’erreur-type). Ce n’est qu’un estimé grossier, mais qui donne une bonne idée quand même.
Deuxièmement, si notre échantillon était très grand, de l’ordre de centaines d’observations, on pourrait ajouter de la précision en utilisant les vraies valeurs de la loi normale. P. ex. dans la distribution normale, 95 % des données se trouvent à 1,96 écart-type de la moyenne (et non 2,0 comme dans le calcul “au pif”).
Enfin, le vrai calcul d’un intervalle de confiance (celui que vous devrez utiliser dans des articles scientifiques, des rapports, etc.) utilise une autre distribution que la loi normale, soit la distribution de T de Student. Cette distribution est définie au Chapitre 12. L’important pour le moment est de savoir qu’elle ressemble beaucoup à la loi normale, mais qu’elle change de forme selon les degrés de liberté de notre échantillon. Avec de grands échantillons, elle se rapproche de la loi normale, mais avec de petits échantillons, elle s’élargit (et donc ajoute de l’incertitude à notre intervalle de confiance). La définition stricte d’un intervalle de confiance à 95 % est donc celle-ci :
\[\bar{x} \pm t_{0,05}\frac{s}{\sqrt{n}}\]
Autrement dit, la valeur de la moyenne ± la valeur de la distribution de T associée à nos degrés de liberté multipliée par l’erreur type.
Notez que ce concept d’erreur-type et d’intervalle de confiance peut s’appliquer aussi à d’autres paramètres de distribution (p. ex. sur la variance).
11.9 Labo : Calculer un intervalle de confiance de façon formelle
Si la moyenne calculée est de 4 et l’erreur-type est de 1,5 et que nous avions 10 observations dans notre échantillon, le calcul serait le suivant pour obtenir les bornes supérieures et inférieures de l’intervalle :
4 + qt(0.975,10-1) * 1.5[1] 7.3932364 + qt(0.025,10-1) * 1.5[1] 0.6067643Il y a plusieurs choses à observer dans ce calcul. Tout d’abord, la fonction qt nous fournit la valeur de t associée à une probabilité et à un degré de liberté. Comme notre intervalle de confiance est bilatéral, il faut penser de séparer le 5 % (100 - 95) de chaque côté de la distribution. Ensuite, nos degrés de liberté sont 10-1, car n est notre nombre d’observations et nous n’estimons qu’un seul paramètre, soit la moyenne. Le 1,5 ici est l’erreur type (soit l’écart-type divisé par la racine carrée de la taille de l’échantillon)
11.10 Exercices
Utiliser les lois de probabilité dans R
Sachant qu’une population de truites pèsent en moyenne 4 kg et que la variabilité dans cette population peut être décrite par une loi normale avec un écart-type de 0,5 kg, répondez à ces quelques question :
À l’aide de la règle du 68-95-99.7, calculez approximativement dans quel intervalle de poids se trouvent 95 % des truites de ce lac.
Vous avez attrapé dans cette population un poisson qui vous paraît exceptionnellement petit à 1,5 kg. À l’aide du logiciel R, calculez la probabilité d’obtenir un poisson de cette taille ou plus petit.
En vous installant pour pêcher, vous remarquez sur l’emballage de vos hameçons que pour offrir un produit à moindre coût, la compagnie tolère 10 % d’hameçons défectueux. Calculez avec R la probabilité d’obtenir aucun hameçon défectueux dans votre emballage de 12 hameçons.
Sachant qu’en moyenne les amateurs pêchent 4 poissons par jour dans ce lac et que la variabilité autour de ce nombre suit un loi de Poisson, quelle est la probabilité que vous attrapiez 10 poissons ou plus en une journée?
Intervalle de confiance - mise en situation
Vous avez été mandatée pour évaluer la productivité d’une forêt boréale. Vous avez donc mesuré la productivité de 8 parcelles, chacune en tonnes par hectare. Voici les chiffres que vous avez obtenus : [7, 11, 8, 12, 10, 9, 7, 9].
Évaluez à partir de cet échantillon la productivité de cette forêt, et l’intervalle de confiance à 99 % de cette estimation. Vous pouvez effectuer vos calculs à l’aide de R.
11.11 Contenu optionnel : L’interprétation stricte d’un intervalle de confiance
Lorsque l’on regarde un intervalle de confiance, p. ex. 5,1 g ± 2,2 g, on est tentés de se dire qu’il y a 95 % des chances que la vraie moyenne se trouve entre ces deux bornes. Dans la vision stricte des statistiques fréquentistes (celles vues dans ce cours, par opposition à l’approche bayésienne entre autres), cette affirmation est fausse. La vraie moyenne est, ou n’est pas dans cet intervalle, mais on ne le sait pas pour cette fois là en particulier.
Le 95 % (ou tout autre chiffre) associé à l’intervalle s’applique en fait à la technique, à l’outil statistique comme tel. Il nous informe qu’en faisant le calcul tel qu’expliqué ci-haut, 95 % du temps on obtiendra un intervalle qui contiendra la vraie moyenne de la population. Pour cette fois-ci en particulier, on a aucun moyen de savoir si la technique a fonctionné ou pas.
Autrement dit, imaginons que vous aviez une immense population d’insectes dont vous connaissez la longueur moyenne et que vous preniez 100 échantillons de 5 individus chacun. Si vous calculiez l’intervalle de confiance de la moyenne sur chacun de ces échantillons, vous en trouveriez probablement 5 dont les bornes ne contiendraient pas la vraie moyenne de votre population.
Page, Scott E. The Model Thinker. 2018 p. 62↩︎