9  Transformer les données

9.1 Introduction

Transformer les données? Non mais Charles, c’est pas comme tricher un peu de transformer nos données? Est-ce qu’on a vraiment le droit de faire ça?

La première chose à savoir pour répondre à cette question est que nos systèmes de mesures sont arbitraires. Ce sont des constructions de notre esprit. Certaines sont à l’échelle directement des données (cm, kg, etc.), mais d’autres sont souvent à des échelles transformées. Entre autres, le pH est défini comme le logarithme négatif de la concentration des ions d’hydrogène (-log[H⁺]). Cette échelle est utilisée quotidiennement, partout dans le monde, bien qu’elle soit une mesure transformée.

L’exemple le plus probant que nos systèmes de mesure sont arbitraires est sans doute la température, où les degrés Fahrenheit peuvent être convertis en degrés Celsius par la transformation (F°-32)*5/9=C°. Clairement, il semble y avoir des cas où il est raisonnable de transformer nos données!

L’important pour qu’une transformation soit utilisable dans un contexte statistique est que la transformation soit monotone (monotonic). C’est-à-dire que l’ordre des observations soit conservé après la transformation. La plus petite donnée doit demeurer la plus petite, la plus grande demeurer la plus grande, etc. Pour autant que cette propriété soit respectée, vous pouvez faire à peu près ce que vous voulez avec les données, sans que cela change les conclusions qualitatives de vos analyses. Lorsque l’on parle de conclusion qualitative, on parle généralement du sens de la relation (A est relié positivement à B, etc) et de son importance (A a un petit effet sur B, C a un grand effet sur B etc.). Évidemment, la conclusion quantitative, le chiffre lui-même définissant notre effet, lui sera différent après la transformation.

J’en profite ici pour vous mentionner que vous pouvez appliquer une transformation différente sur chacune des variables de votre tableau de données. Il n’est pas nécessaire que chaque variable subisse la même transformation. Il est même possible d’avoir certaines variables transformées et d’autres non, cela n’a pas d’importance.

9.2 Pourquoi transformer

La raison majeure pour laquelle nous utilisons des transformations en statistiques est pour forcer des données dans un modèle lorsque ces dernières ne respectent pas les assomptions de l’outil statistique. On peut, par une transformation, normaliser des données qui n’étaient pas normales ou linéariser une relation qui n’était pas linéaire. On peut aussi utiliser une transformation pour diminuer l’effet d’une valeur aberrante sur une analyse, en la rapprochant du nuage de points principal.

9.3 Labo : La transformation logarithmique

La transformation que vous utiliserez sans doute le plus souvent est la transformation logarithmique. On entend par une transformation logarithmique que chacune des observations d’une variable soit remplacée par le logarithme de cette observation. Le base du logarithme n’a pas vraiment d’importance d’un point de vue statistique. Vous pouvez donc utiliser un log₁₀, log_e, log₂, comme vous voulez.

À titre de rappel, le logarithme est la réponse à la question : combien de fois doit-on multiplier la base du logarithme par elle-même pour arriver au nombre attendu. Par exemple, log₂(8) = 3. On doit faire 2 x 2 x 2 pour arriver à 8. De la même façon, log₁₀(100)=2, car 10 x 10 = 100, etc.

Pour ce chapitre, nous travaillerons avec le tableau de données msleep fourni avec la librairie ggplot2 plutôt que nos manchots habituels, puisque le tableau msleep contient beaucoup de variables qui vaudront la peine d’être transformées. Dans ce tableau, chaque ligne représente une espèce. Nous avons plusieurs colonnes contenant des information sur le temps de sommeil des différentes espèces, mais aussi certaines informations sur des mesures physiologiques, soit le poids du corps (bodywt) et le poids du cerveau (brainwt)

On peut par exemple se créer une colonne du poids du cerveau et du corps de chaque animal en log base e, comme ceci :

library(tidyverse) 
msleep |> 
  mutate(
    log_bodywt = log(bodywt),
    log_brainwt = log(brainwt)
  )

Cependant, avant d’appliquer une transformation, il importe de bien comprendre les maths derrière cette dernière. Par exemple, dans le cas de la transformation log, le log des valeurs <= 0 n’est pas défini. Il est donc important de vérifier que toutes nos valeurs sont > 0 avant d’appliquer cette transformation. Si la condition n’est pas respectée, il est possible de les déplacer légèrement en ajoutant une constante avant la transformation, par exemple comme ceci :

msleep |>
  mutate(
    log_bodywt = log(bodywt+1),
    log_brainwt = log(brainwt+1)
  )

Alors, que fait la transformation log à nos données? Ce qu’il est important de retenir est que cette transformation étire les petites valeurs et compresse les grandes. Si l’on prend une série de valeurs également espacées, voici à quoi elles ressembleront après une transformation log :

Une fois que cette propriété est bien comprise, il devient intuitif de comprendre que cette transformation pourra normaliser (i.e. donner une forme normale) une distribution qui présentait à l’origine une longue queue à droite, comme ceci :

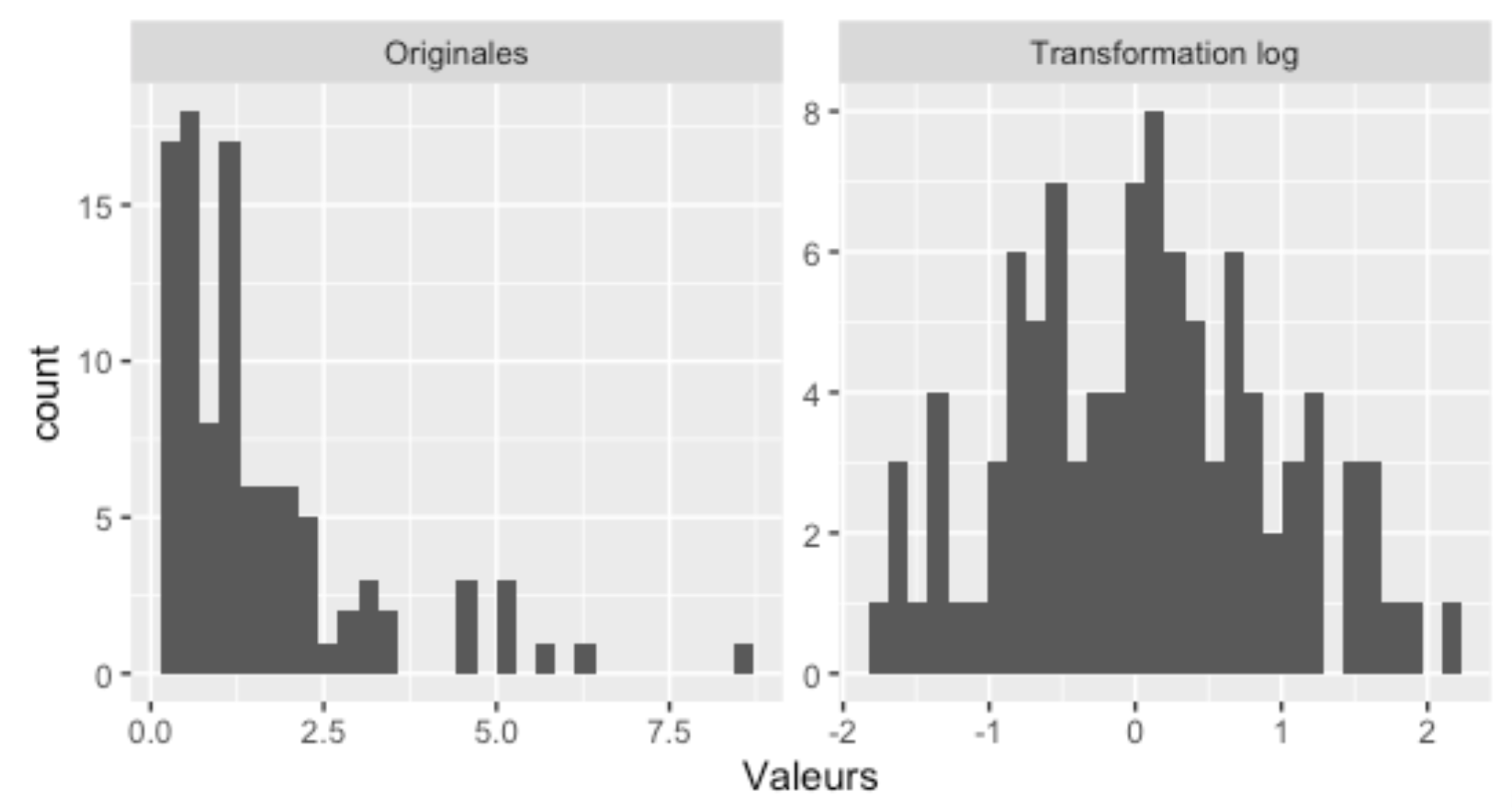
Remarquez que cette transformation log aura aussi pour effet de rapprocher les valeurs que l’on aurait pu considérer comme aberrantes dans les données originales, pour autant que celles-ci étaient à la droite de la distribution.

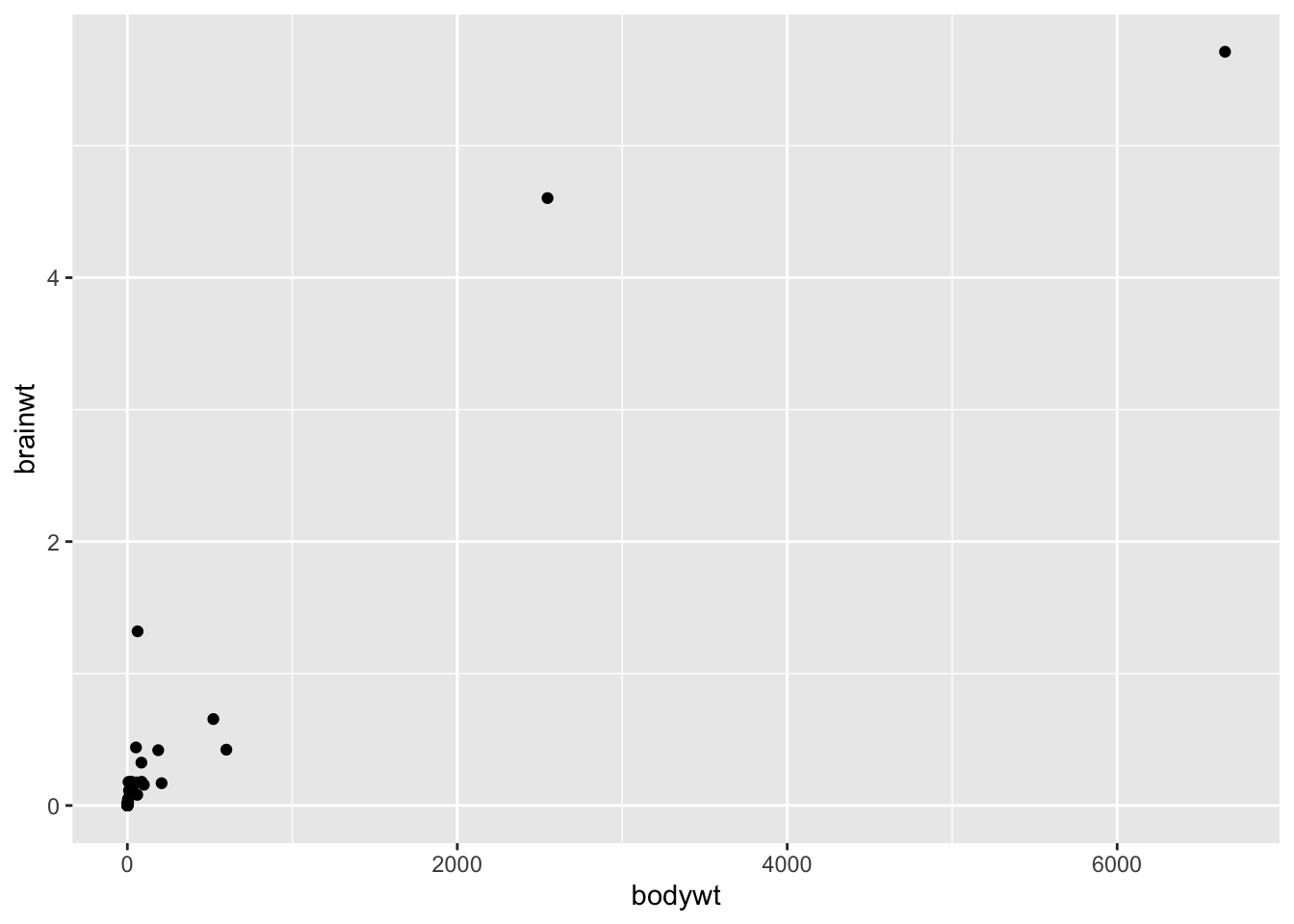
Dans le même ordre d’idées, la transformation log peut aussi permettre de linéariser une relation, qui autrement aurait été de nature exponentielle. Comparez par exemple les courbes générées par la relation entre brainwt et bodywt dans le tableau de données msleep avec les données originales :

Puis avec les deux variables transformées en log :

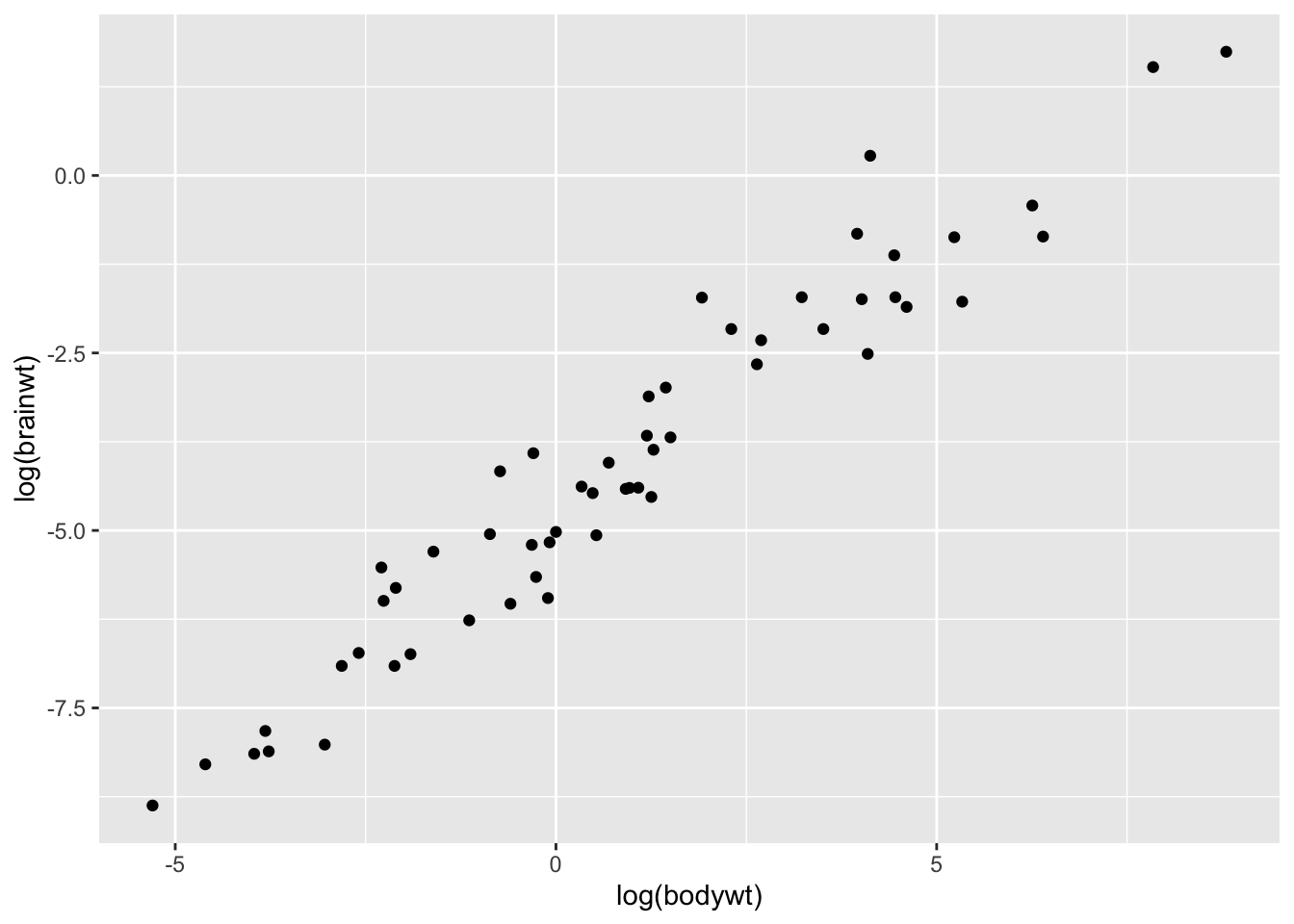
Encore une fois, la clé pour comprendre cet effet est de réaliser que la transformation étire les petites données, et compresse les grandes.

9.4 Labo : La transformation racine carrée

La transformation racine carrée a des effets très semblables à la transformation logarithmique, mais son effet est moins prononcé. Donc, dans un scénario où la distribution de votre variable présentait une longue queue à droite, mais que la transformation log, plutôt que normaliser a créé une longue queue à gauche (i.e. elle sur-corrige), la transformation racine carrée sera peut-être appropriée. Rappelez-vous, cependant, qu’avant d’appliquer une transformation racine carrée, il importe de bien inspecter vos données, puisqu’une racine carrée n’est pas définie pour les nombres négatifs…

Dans R, la transformation racine carrée (sqrt; SQuare RooT) s’applique comme ceci :

msleep |>
  mutate(
    sqrt_bodywt = sqrt(bodywt)
  )

Si jamais vos données présentent une longue queue à droite, mais que ni la transformation racine carrée ni la transformation log ne présentent le résultat escompté, rappelez-vous qu’une racine carrée est équivalente à appliquer l’exposant ½ à vos données.

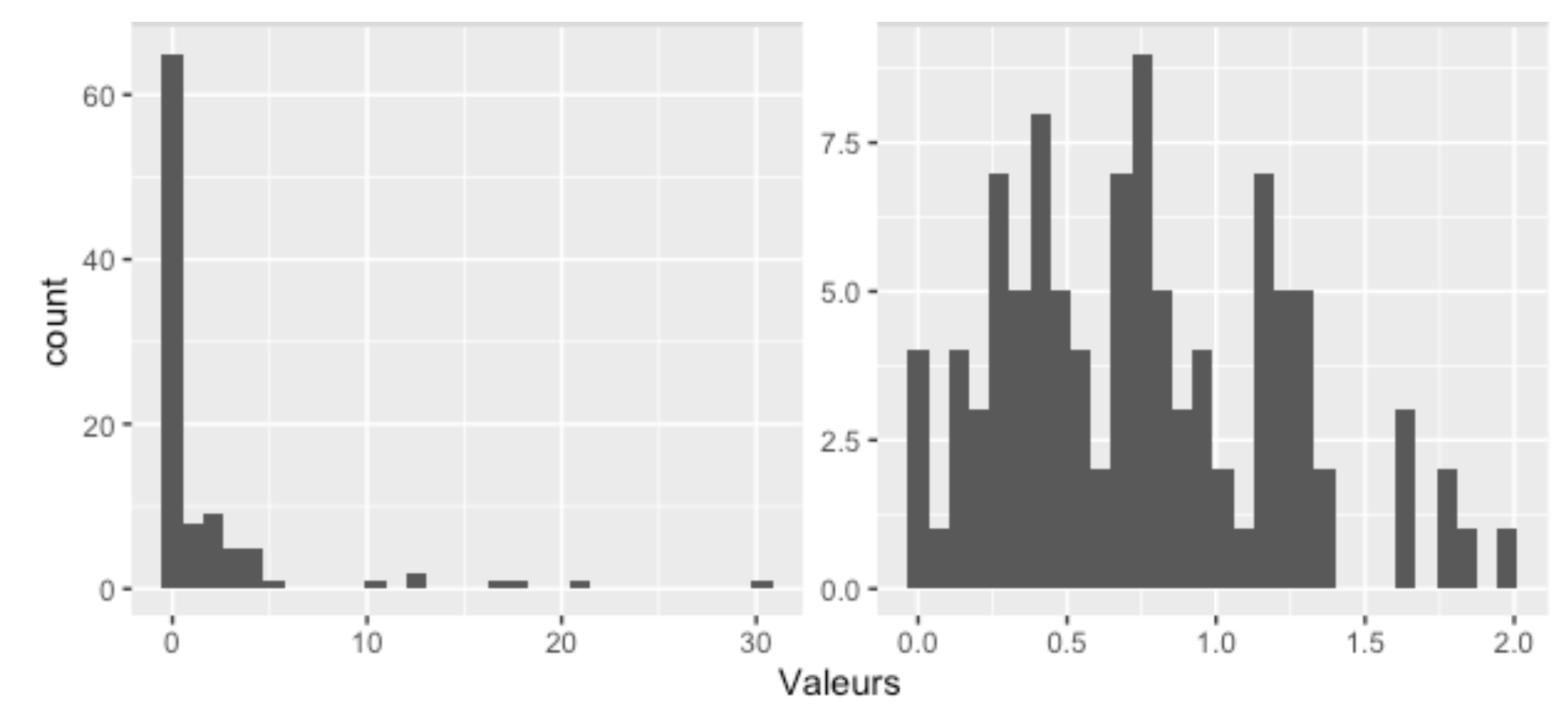
Sachant cela, il est possible d’appliquer en fait n’importe quel exposant fractionnaire à nos données, pour obtenir exactement la transformation voulue. Voyez par exemple ces données présentant une queue très prononcée à droite, qui peuvent être normalisées à l’aide de l’exposant ⅕ (0,2) :

Soyez cependant bien attentif lorsque vous appliquez un exposant fractionnaire à vos données dans R. L’opérateur d’exposant ayant préséance sur celui de division dans l’ordre des opérations, la façon correcte d’appliquer un exposant fractionnaire est à l’aide de parenthèses, comme ceci :

msleep |> 
  mutate(
    trans_bodywt = bodywt^(1/4)
  )

Rappelez-vous aussi en faisant vos transformations que la forme de votre distribution finale ne sera jamais parfaitement normale, ce qui n’est pas nécessairement grave car la plupart des analyses sont robustes à la non-normalité.

9.5 Si la longue queue est à gauche

Toutes les transformations vues jusqu’à présent permettent de corriger des problèmes avec nos données lorsque celles-ci sont asymétriques avec une longue queue à droite. Si la longue queue est à gauche, on peut utiliser le même principe des exposants, mais en utilisant des valeurs supérieures à un. Par exemple, voici l’effet de l’exposant 4 à des données présentant une longue queue à gauche :

9.6 Exercice : Les transformations

Dans le tableau de données msleep, affichez l’histogramme de fréquences de la variable sleep_rem, puis tentez de déterminer quelle serait la meilleure transformation pour normaliser cette variable pour une analyse.

Dans le même tableau de données, visualisez la forme de la relation entre les variables sleep_rem et (en X) et sleep_total (en Y). Vous pouvez ajouter une courbe de lissage (geom_smooth) pour mieux voir la forme de la relation. Quelle serait la meilleure transformation à appliquer aux variables pour linéariser cette relation?

NB : ne désespérez pas si vous ne réussissez pas à bien transformer vos variables du premier coup. Il s’agit d’un processus essai-erreur, qui s’accélérera à mesure que vous pratiquerez.