3  Voir les données

3.1 Piloter à vue

Une des choses les plus importantes que vous aurez à faire lors de vos analyses statistiques est de visualiser les données. Pierre Magnan, qui m’a enseigné le cours de Biologie Quantitative à l’époque, aimait bien comparer les statistiques au pilotage d’avion. Il répétait toujours que voir les données, c’est comme regarder par la fenêtre de l’avion pour voir ce qu’il y a autour. Avant de regarder les chiffres sur les cadrans, il est primordial de voir où l’on va, de connaître les obstacles. De même, en statistiques, il est important de toujours voir ce que l’on fait. Si vos yeux voient une chose et que les chiffres en disent une autre, croyez d’abord vos yeux et doutez des chiffres.

À titre d’illustration, observez ces quatre relations classiques décrites par Anscombe :

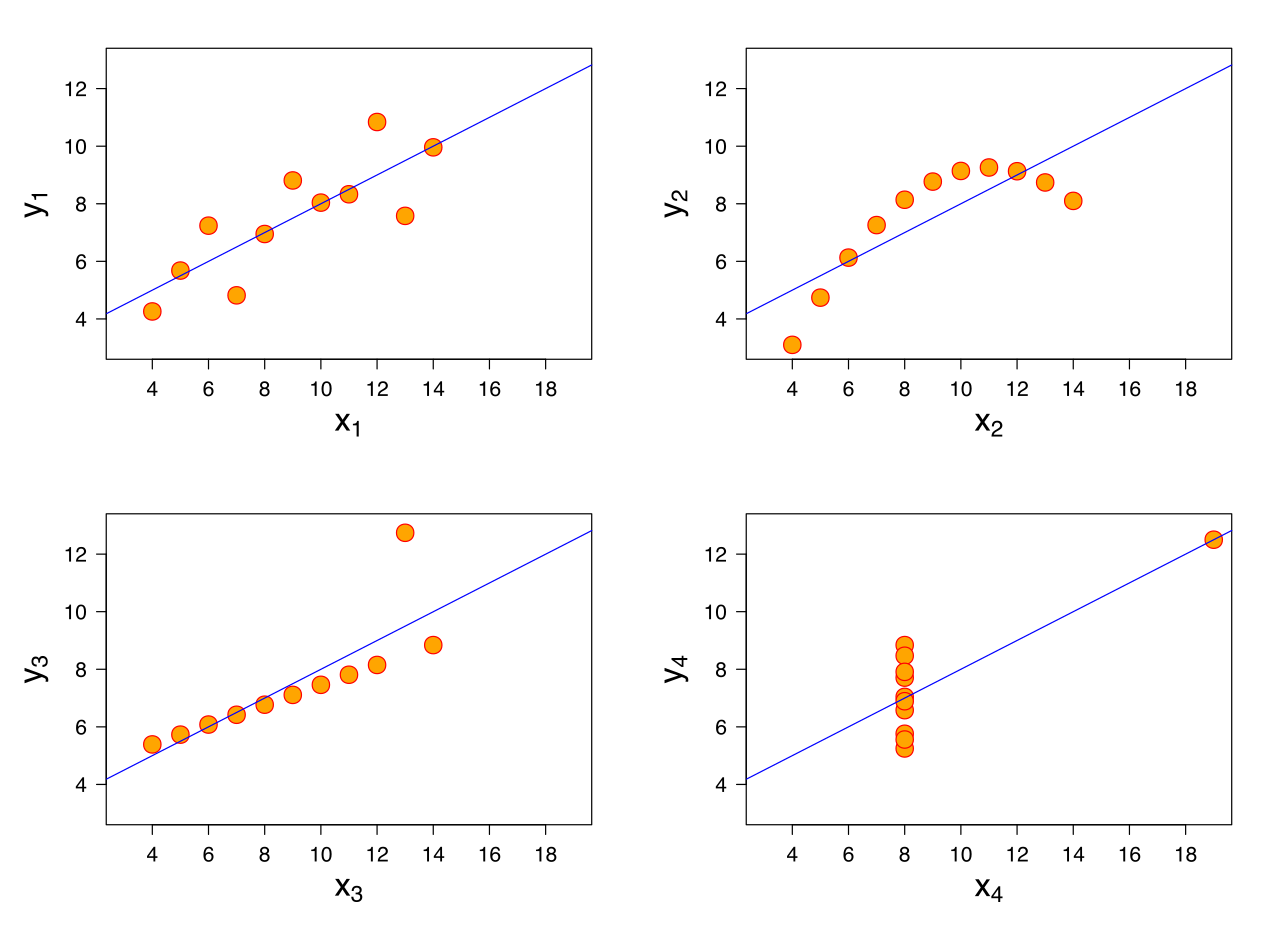
Anscombe.svg: Schutz Avenue, CC BY-SA 3.0, via Wikimedia Commons

Bien que ces relations correspondent à des réalités complètement différentes, la grande majorité de leurs propriétés statistiques sont identiques. Elles présentent, entre autres, la même moyenne des X, la même moyenne des Y, la même variance des X et la même variance des Y (voir Section 5.2). Elles ont aussi la même corrélation (voir Chapitre 17), et la pente calculée par une régression linéaire donnerait exactement le même résultat (voir Chapitre 18). Gardez bien cette illustration en tête. Elle doit être un rappel constant que calculer des statistiques sans voir les données peut être extrêmement hasardeux, voire même dangereux

Il peut évidemment arriver des cas pointus, dans des modélisations complexes, où l’on pourra trouver des choses qui nous avaient échappé au moment de l’exploration visuelle, mais comme pour le pilotage d’avion aux instruments dans le brouillard, il faut avoir beaucoup d’expérience au pilotage à vue avant d’en arriver là.

3.2 Les différents types des données

Avant de lancer R pour regarder des données, nous aurons besoin de définir les différents types de données que nous pourrons rencontrer, car nous y reviendrons fréquemment.

La première distinction à faire est entre les données quantitatives et les données qualitatives. Une donnée quantitative est une donnée à laquelle nous pouvons associer un chiffre : un arbre mesurant 30 cm de diamètre, un oiseau pesant 12 g, un nid contenant 6 oeufs. À l’inverse, une donnée qualitative n’a pas de chiffre associé : la couleur de vos yeux, la ville où vous êtes né, le nom du lac où un poisson a été capturé. Il s’agit de la distinction la plus importante.

Remarquez que souvent, les variables qualitatives sont des raccourcis, des généralisations, qu’il serait plus juste ou nuancé de décrire sur un gradient. La couleur des yeux, pourrait par exemple être décrite plus précisément à l’aide d’un triplet de variables quantitatives décrivant la quantité de rouge, de vert et de bleu (le fameux RGB1) plutôt que par un nom de couleur.

On peut par la suite diviser les données quantitatives en deux groupes : quantitatives continues et quantitatives discrètes. Les données quantitatives continues sont celles où, si notre instrument de mesure était plus précis, nous aurions pu ajouter des décimales à notre nombre. Pensons à un oiseau pesant 12 g. Avec une balance plus précise, nous aurions peut-être su qu’il pesait 12,5 g ou 12,47 g. Les données quantitatives discrètes quant à elles ne peuvent être rien d’autres que des entiers. Par exemple le nombre d’œufs dans un nid, le nombre de graines dans un sac, etc.

Notez qu’il est possible, avec un peu de mauvaise foi (ou de malchance!) d’obtenir 0,5 œuf dans un nid. Il peut être aussi possible de passer d’une échelle qualitative à une échelle quantitative et vice versa, par exemple en passant de présence/absence à 0/1 ou l’inverse. Mais nous ne nous compliquerons pas la vie pour le moment avec ces cas plus pointus.

3.3 Labo : Préparatifs

Plutôt que d’utiliser les graphiques de base de R, nous utiliserons la très populaire librairie ggplot2. Cette dernière a été conçue pour implémenter ce que les auteurs ont nommé la grammaire des graphiques. Autrement dit, leur but est de nous fournir un vocabulaire nous permettant de décrire ce que l’on veut présenter dans nos graphiques.

Comme à la section suivante, nous devrons donc installer cette librairie externe avant de commencer à travailler :

install.packages("ggplot2")

Pour commencer à travailler, nous devrons ensuite activer cette librairie, de même que celle contenant nos données de manchots :

library(ggplot2)
library(palmerpenguins)
Astuce

Bien qu’il puisse être tentant (et rapide!) de copier-coller le code fournit dans ce livre, je vous conseille fortement d’écrire le code vous même dans la console de R. Vous retiendez beaucoup mieux l’information. Vous ferez bien sûr quelques erreurs supplémentaires se faisant, mais apprendre à reconnaître et corriger nos erreurs fait aussi partie des compétences à acquérir pour être confortable dans R. Autant le faire dès le début, dans des exemples simples.

3.4 Labo : Les types de données dans R

Les types de données décrits ci-hauts ont leurs équivalent dans le logiciel R. Voyons d’abord ce qui se produit lorsque l’on envoit le nom d’un tableau de données dans la console de R :

penguins
# A tibble: 344 × 8
   species island    bill_length_mm bill_depth_mm
   <fct>   <fct>              <dbl>         <dbl>
 1 Adelie  Torgersen           39.1          18.7
 2 Adelie  Torgersen           39.5          17.4
 3 Adelie  Torgersen           40.3          18  
 4 Adelie  Torgersen           NA            NA  
 5 Adelie  Torgersen           36.7          19.3
 6 Adelie  Torgersen           39.3          20.6
 7 Adelie  Torgersen           38.9          17.8
 8 Adelie  Torgersen           39.2          19.6
 9 Adelie  Torgersen           34.1          18.1
10 Adelie  Torgersen           42            20.2
# ℹ 334 more rows
# ℹ 4 more variables: flipper_length_mm <int>,
#   body_mass_g <int>, sex <fct>, year <int>

La première ligne nous informe que notre objet est de type tibble. Les tibbles sont un type de tableau de données dans R. Vous verrez aussi souvent des tableaux de données de type data.frame, qui se traitent de façon très semblable.

Cette ligne nous informe ensuite que notre tableau contient 344 lignes et 8 colonnes.

Les deux lignes suivantes nous donnent ensuite la liste des colonnes (species,island, bill_length_mm, etc.) et le type associé à chaque des colonnes (fct, fct, dbl, etc.)

Enfin, on a les valeurs pour chacune des lignes et colonnes du tableau.

Par défaut, un objet de type tibble ne nous montre qu’un aperçu intéressant qui entre correctement dans notre écran.

C’est pourquoi vous voyez au bas du tableau la mention 334 more rows et 4 more variables ....

Pour les tableaux dédiés à l’analyse, R contient les 3 mêmes types de données que décrits plus haut, soit

  • double (dbl) pour les données quantitatives continues
  • integer (int) pour les données quantitatives discrètes et
  • factor (fct) pour les données qualitatives.

Vous verrez aussi parfois le type character (chr) pour des données textuelles, qui ne sont pas encore considérées comme des variables qualitatives (nous en reparlerons au Chapitre 15).

Vous pouvez connaître le type de toutes les variables d’un tableau de données avec la fonction str (pour structure) :

str(penguins)
tibble [344 × 8] (S3: tbl_df/tbl/data.frame)
 $ species          : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...
 $ island           : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...
 $ bill_length_mm   : num [1:344] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...
 $ bill_depth_mm    : num [1:344] 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...
 $ flipper_length_mm: int [1:344] 181 186 195 NA 193 190 181 195 193 190 ...
 $ body_mass_g      : int [1:344] 3750 3800 3250 NA 3450 3650 3625 4675 3475 4250 ...
 $ sex              : Factor w/ 2 levels "female","male": 2 1 1 NA 1 2 1 2 NA NA ...
 $ year             : int [1:344] 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...

Enfin, vous pouvez aussi explorer vos données de façon plus conventionnelle avec la fonction View :

View(penguins)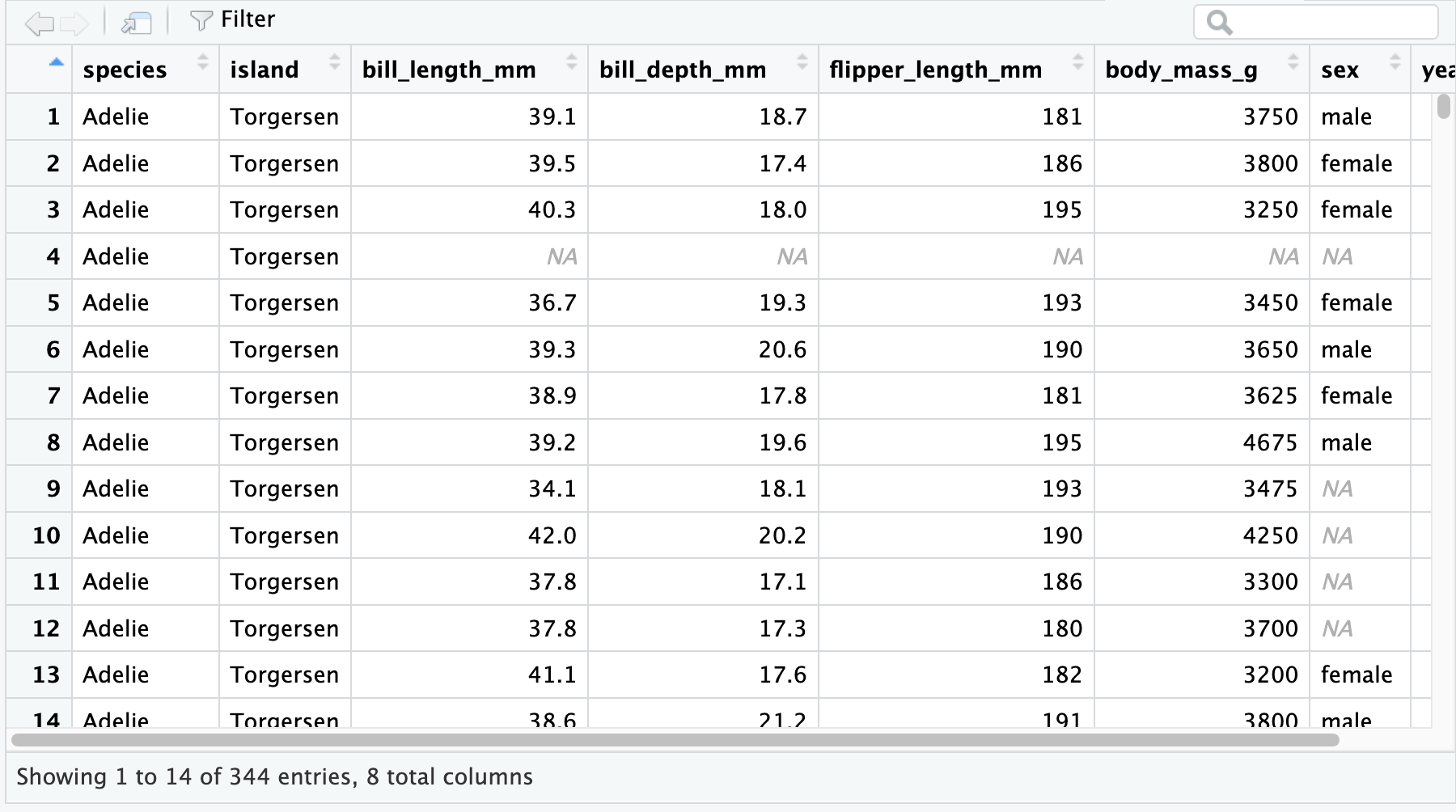

Il est important de mentionner à ce moment-ci que R est un langage de programmation sensible à la casse, c’est-à-dire qu’il faut faire attention aux majuscules et aux minuscules lorsque l’on entre des commandes. Jusqu’à ce point, nous avons tout écrit en minuscules, mais la fonction View, elle, doit être écrite avec la première lettre en majuscule!

Observez bien la structure de la commande précédente. Elle contient deux éléments, le premier (View) est le nom de la fonction que nous voulons lancer. Les fonctions sont toujours accompagnées de parenthèses. Les parenthèses contiennent les arguments que l’on veut donner à la fonction, pour contrôler son fonctionnement. Ici, nous lui avons passé l’objet penguins. Nous avons donc demandé à R de voir (to view) notre tableau de données de manchots (penguins).

3.5 Labo : Un premier graphique

Maintenant que ces préliminaires sont derrière nous, lançons le code qui créera notre premier graphique :

ggplot(data = penguins) +
  geom_point(mapping = aes(x = flipper_length_mm, y = body_mass_g))
Warning: Removed 2 rows containing missing values or values
outside the scale range (`geom_point()`).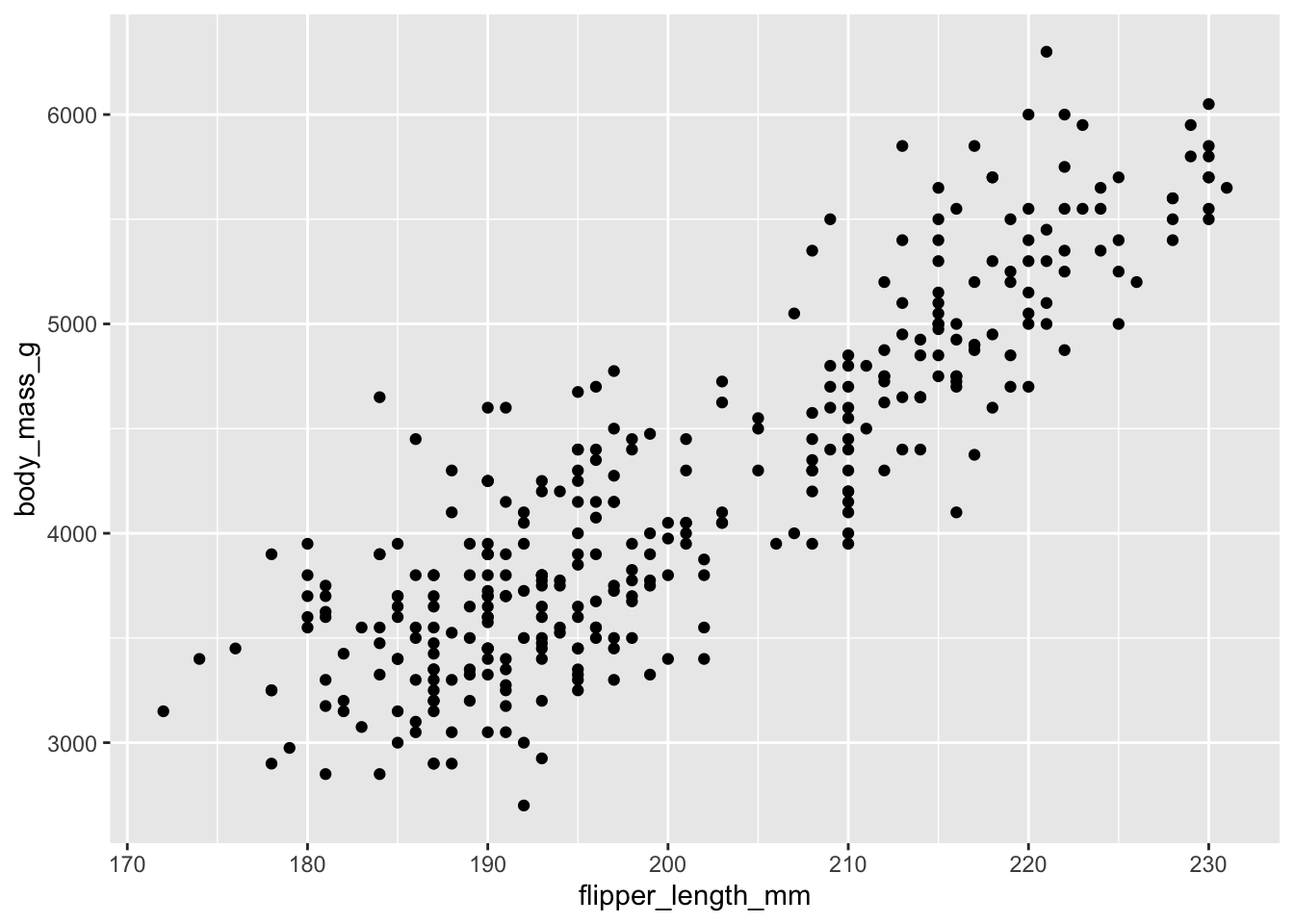

Ce graphique nous montre la relation entre deux variables de notre tableau de données soit la longueur des ailes en X et le poids en Y.

Analysons tranquillement les morceaux de code qui ont permis de construire ce graphique. Sur la première ligne, on reconnaît une fonction (ggplot) et un argument (data = penguins). Tous vos graphiques de ggplot démarreront par cette fonction. C’est elle qui crée la base du graphique. L’argument data=penguins informe R que dans ce graphique, nous utiliserons des variables provenant du tableau de données penguins  Contrairement à notre premier exemple avec View, notre argument penguins possède un nom (data=) qui indique à la fonction ggplot à quoi cet objet servira. Dans certains cas, on peut se permettre de ne pas nommer l’argument, mais nous commencerons par tous les nommer, question de clarté.

Cette première ligne se termine par le symbole +, pour indiquer à R que nous voulons ajouter des choses à ce graphique. Sur la ligne suivante, nous appelons la fonction geom_point. Cette fonction ajoute une couche à notre graphique. Toutes les couches graphiques de ggplot débutent par le préfixe geom_. Nous verrons plus loin qu’il en existe des dizaines d’autres. Dans ce cas particulier, nous avons demandé une couche de points. L’intérieur de la parenthèse sert ensuite à expliquer à R quoi mettre dans notre couche de points. L’argument mapping nous permet d’associer (to map) des propriétés du graphiques à des variables de notre tableau de données. On informe R qu’en X, nous voulons les valeurs de la variable flipper_length_mm, et en Y, nous voulons les valeurs de la variable body_mass_g.

La structure d’un graphique avec ggplot2 consiste donc à un appel à la fonction ggplot, auquel on associe notre tableau de données. On peut ensuite ajouter une (ou plusieurs) couche graphique (nommées geom_) dans laquelle on connecte les propriétés du graphique à celles du tableau de données. Il est capital de bien comprendre cette structure car elle se répètera pour tous vos graphiques avec cette librairie.

Vous aurez aussi peut-être remarqué que R, après avoir fait le graphique nous indique le message suivant :

Warning: Removed 2 rows containing missing values or values
outside the scale range (`geom_point()`).

Pour le moment, cet avertissement est normal. R nous avertit qu’il y a 2 des lignes de notre tableau de données qui n’ont pas pu être affichées parce que une des variables demandée contenait des données manquantes. Nous verrons au Chapitre 4 comment filtrer ces données pour éliminer ce genre de messages.

3.6 Labo : Les propriétés graphiques

Nous avons vu dans notre premier exemple deux propriétés graphiques, soit les coordonnées X et Y d’un point. Il en existe plusieurs autres. Pour la couche de points (geom_point), vous avez accès, entre autres, à :

  • color (la couleur du point)
  • size (la taille du point)
  • alpha (l’opacité, allant de 0 à 1)
  • shape (maximum 6 formes)
  • fill (la couleur de remplissage de certaines formes)

Pour obtenir de l’information sur une fonction dans R, vous pouvez taper l’opérateur “?” suivi du nom de votre fonction dans la console, p. ex. :

?geom_point

RStudio vous affiche alors dans le panneau Help l’aide de la fonction. Vous voyez entre autres dans cette aide la section Arguments, qui vous donne la liste de tous les arguments qui peuvent être acceptés par cette fonction. Pour les couches de ggplot2, vous avez aussi accès à une section Aesthetics, qui contient la liste des propriétés de la couche auxquelles vous avez accès dans le mapping.

Mettons ces connaissances en pratique dans un deuxième graphique :

ggplot(data = penguins) +
  geom_point(mapping = aes(
    x = flipper_length_mm,
    y = body_mass_g,
    color = species,
    size = bill_length_mm
  )
)
Warning: Removed 2 rows containing missing values or values
outside the scale range (`geom_point()`).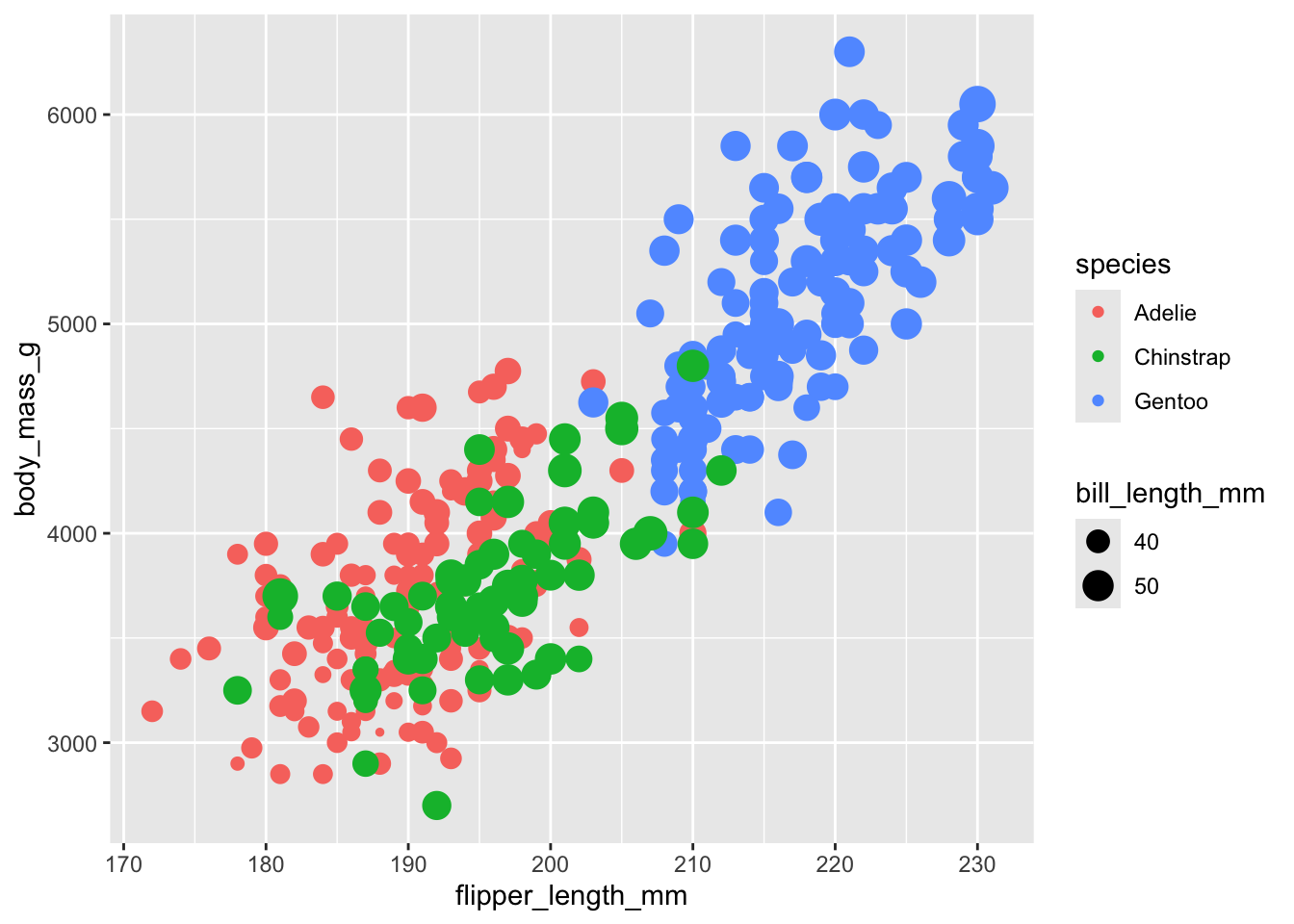

Dans cet exemple, nous avons utilisé 4 propriétés graphiques : X et Y sont associés, comme dans l’exemple précédent, à flipper_length_mm et body_mass_g, mais l’espèce (species) est maintenant associée à la couleur et la longueur du bec (bill_length_mm) est associée à la taille du point. Nous affichons donc 4 informations différentes par point. Notez que ggplot2 a ajouté pour vous les légendes pour les propriétés graphiques supplémentaires.

Si jamais vous voudriez modifier une des propriétés graphiques pour l’ensemble des points plutôt que de se baser sur les valeurs d’une variable, il faut simplement sortir cet argument du mapping, et mentionner directement la valeur désirée, p. ex. :

ggplot(data = penguins) +
  geom_point(
    mapping = aes(
      x = flipper_length_mm,
      y = body_mass_g,
      size = bill_length_mm
    ),
    color = "blue",
    shape = "triangle"
)
Warning: Removed 2 rows containing missing values or values
outside the scale range (`geom_point()`).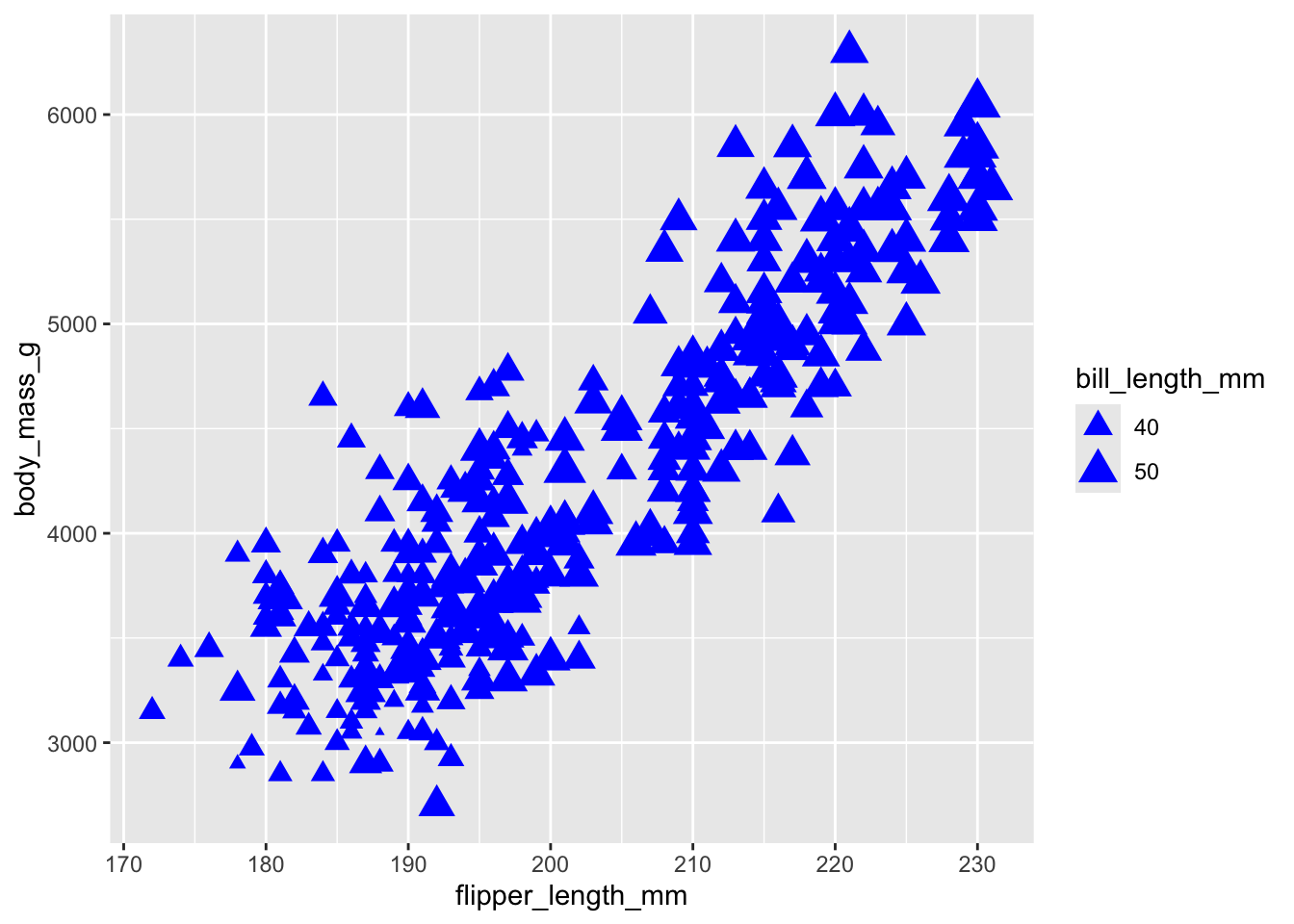

Observez bien que X et Y sont toujours dans la parenthèse du mapping, alors que color et shape sont maintenant à l’extérieur. Remarquez que le nom de la couleur doit être mentionné entre guillemets et inscrit en anglais. La plupart des noms de couleurs qui vous viendront en tête sont déjà définis dans R, mais en cas de doutes, vous pouvez facilement trouver la liste des couleurs disponibles sur internet2.

Pour les formes, elles peuvent aussi être nommées avec leur nom anglais, par exemple “square open”, “cross”, etc. La liste complète des noms de formes peut se trouver ici : https://github.com/tidyverse/ggplot2/pull/2338. Cette façon de faire, plus récente, est par contre moins connue et moins documentée que celle qui a longtemps prévalu, soit d’utiliser des numéros de formes3.

3.7 Labo : Choisir la bonne couche graphique

Il existe dans ggplot2 des dizaines de couches permettant de concevoir à peu près tous les graphiques imaginables. La difficulté consistera surtout à déterminer quelle couche graphique utiliser dans chaque situation, selon le type de données et ce que l’on veut montrer. Nous en verrons cinq principales, qui devraient satisfaire l’ensemble de nos besoins.

La distribution d’une variable quantitative

La première couche graphique que nous explorerons est l’histogramme de fréquences. L’histogramme est utile pour visualiser la distribution des valeurs d’une variable quantitative dans notre tableau de données. Il permet de savoir quelles valeurs sont communes et quelles valeurs sont rares. On peut, avec ggplot2 créer un histogramme en utilisant la couche graphique geom_histogram :

ggplot(data = penguins) +
  geom_histogram(mapping = aes(x = body_mass_g))
`stat_bin()` using `bins = 30`. Pick better value with
`binwidth`.
Warning: Removed 2 rows containing non-finite outside the scale
range (`stat_bin()`).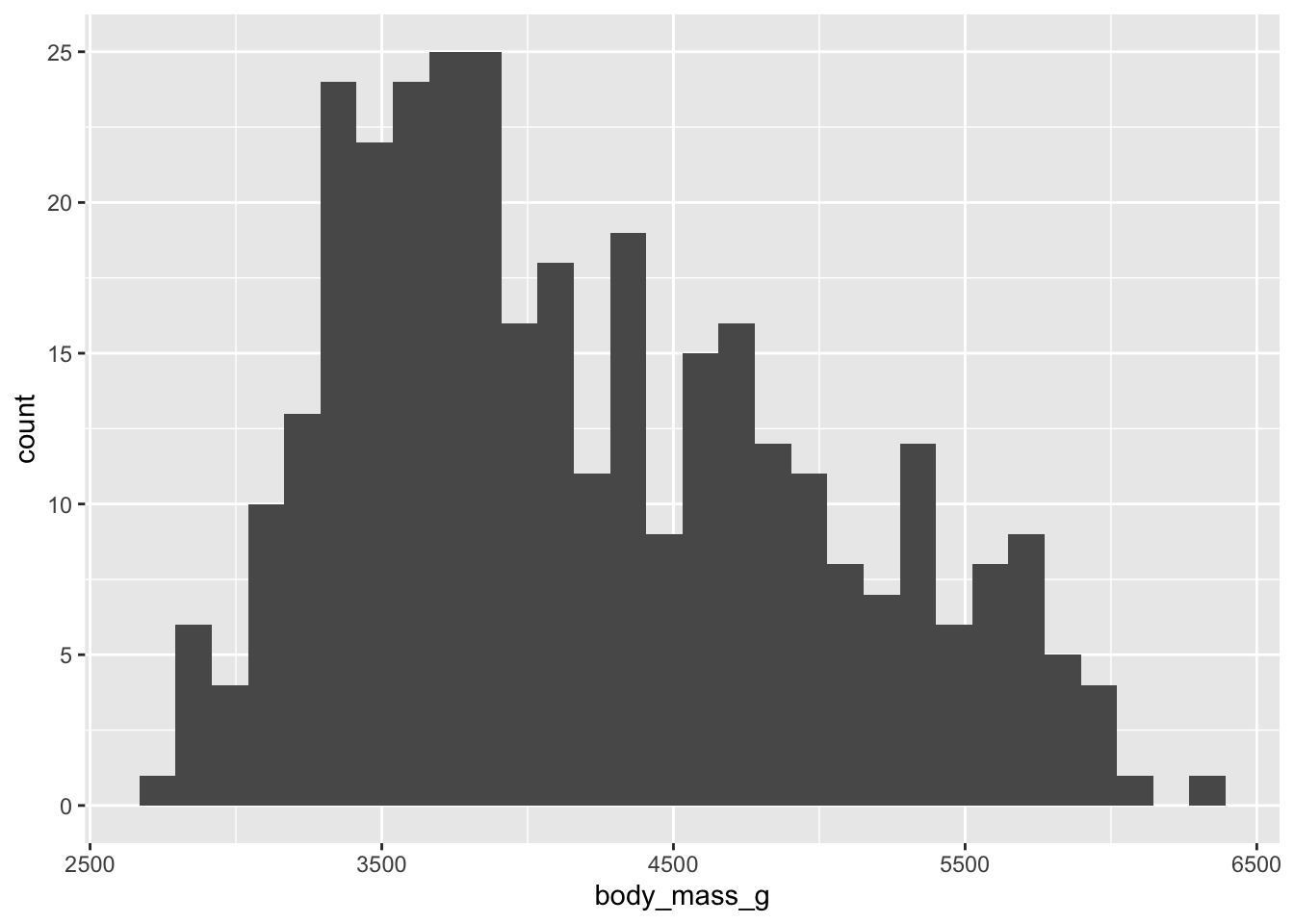

Dans un histogramme, l’axe des X est découpé par classes (bins), de largeurs égales. La hauteur de chaque bande (axe des Y) correspond au nombre d’observations de chaque classe de variable (leur fréquence). Dans notre exemple, la première classe (à gauche) contient par exemple 1 valeur, la deuxième en compte 6 et la plus commune en compte 25.

Notez que par défaut, ggplot2 choisit de créer 30 classes. C’est un nombre tout à fait arbitraire, qu’il vaut la peine de modifier pour voir si notre impression des données change. On peut modifier le nombre de classes avec l’argument bins, qu’il faut prendre soin de mettre à l’extérieur du mapping, p. ex. :

ggplot(data = penguins) +
    geom_histogram(
        mapping = aes(x = body_mass_g), 
        bins = 100
    )
Warning: Removed 2 rows containing non-finite outside the scale
range (`stat_bin()`).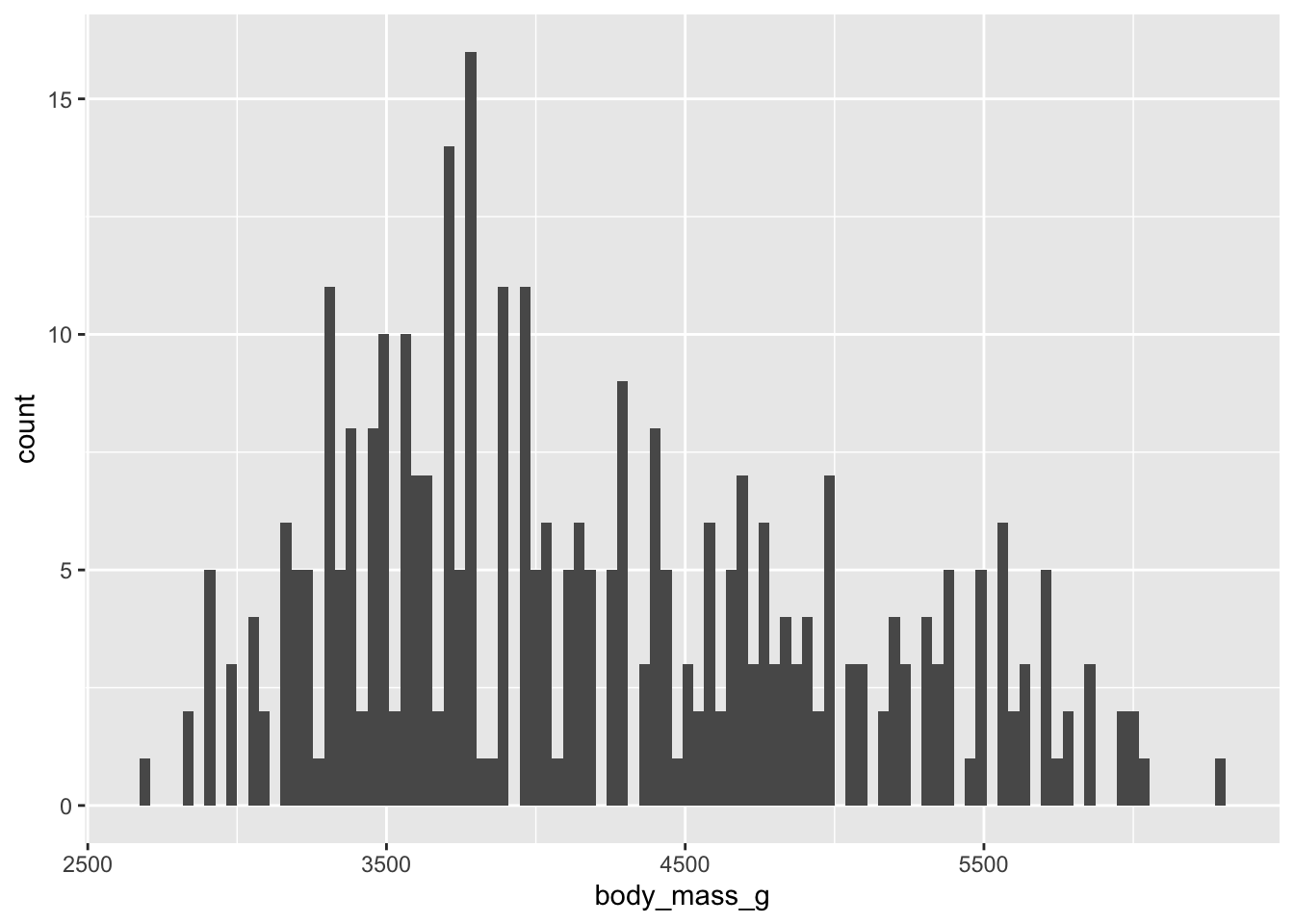

Vous verrez aussi parfois un histogramme avec un axe des Y différent, qui affiche les fréquences relatives plutôt que les fréquences absolues. La fréquence relative se définissant pour chaque classe comme le nombre d’observations dans cette classe, divisé par le nombre total d’observations.

La distribution d’une variable qualitative

Le deuxième graphique que nous verrons est très semblable à l’histogramme, il se nomme diagramme à bandes. Le diagramme à bandes permet de voir comment se répartissent les observations d’une variable qualitative (plutôt que quantitative dans le cas de l’histogramme). La couche de diagramme à bandes dans ggplot2 se nomme geom_bar :

ggplot(data = penguins) +
  geom_bar(mapping = aes(x = species))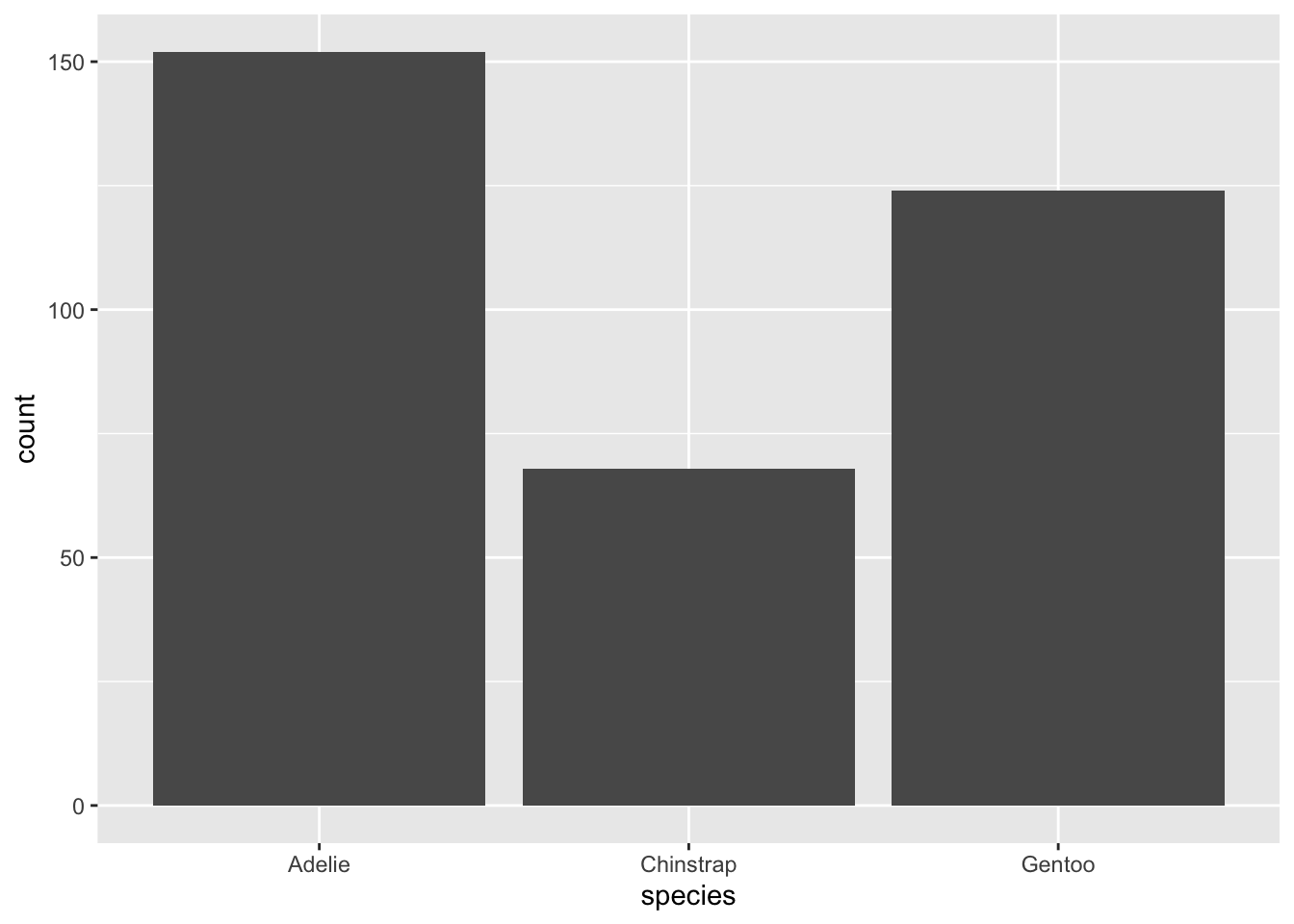

On peut voir dans ce graphique que l’espèce la plus commune dans ces données est le manchot Adélie, et la plus rare est le manchot Chinstrap.

Notez enfin que dans le cas du diagramme à bandes, il existe visuellement un espace entre les bandes, alors qu’elles sont collées les unes sur les autres dans l’histogramme.

Prenez garde que la couche geom_bar s’attend à calculer elle-même le nombre d’observations pour chacune des bandes. Pour qu’elle fonctionne correctement, vos données doivent être organisées comme ceci :

species
Adelie
Chinstrap
Adelie
…

Si jamais la fréquence pour chaque bande est déjà calculée, par exemple comme cela :

species n
Adelie 152
Chinstrap 68
Gentoo 124
… …

Il faut plutôt utiliser la couche geom_col :

ggplot(data = tableau_deja_calcule) +
  geom_col(mapping = aes(x = species, y = n))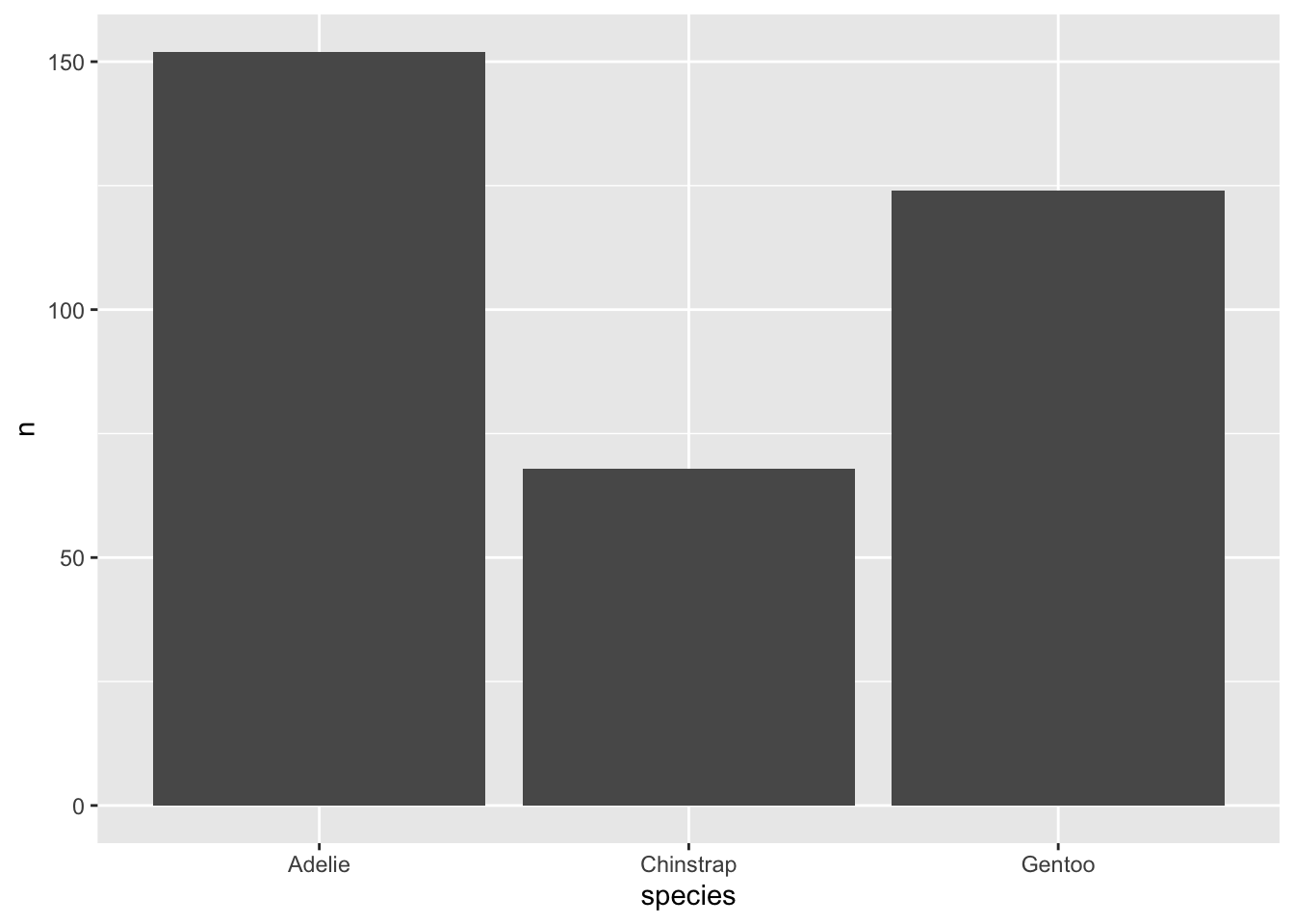

Si jamais vous voulez faire fonctionner l’exemple précédent, vous devez d’abord créer un tableau de données nommé tableau_deja_calcule, par exemple comme ceci :

library(dplyr)
tableau_deja_calcule <- 
  penguins |> 
  count(species)

Ce genre de code, très compact, sera détaillé à la Section 6.3 et nécessite l’installation de la librairie dplyr.

Ces deux couches (histogramme et diagramme à bandes) graphiques nous étaient utiles pour observer nos variables une à la fois. Nous allons maintenant voir quelles couches graphiques sont disponibles pour regarder l’association ou la relation entre deux variables différentes.

La relation entre deux variables quantitatives

Si nous voulons regarder l’association entre deux variables quantitatives, la façon classique de le faire est à l’aide d’un nuage de points (scatterplot). La couche graphique pour les nuages de points dans ggplot2 est le geom_point, dont nous avons vu plusieurs exemples au début de ce chapitre. Par exemple :

ggplot(data = penguins) +
  geom_point(mapping = aes(x = flipper_length_mm, y = body_mass_g))
Warning: Removed 2 rows containing missing values or values
outside the scale range (`geom_point()`).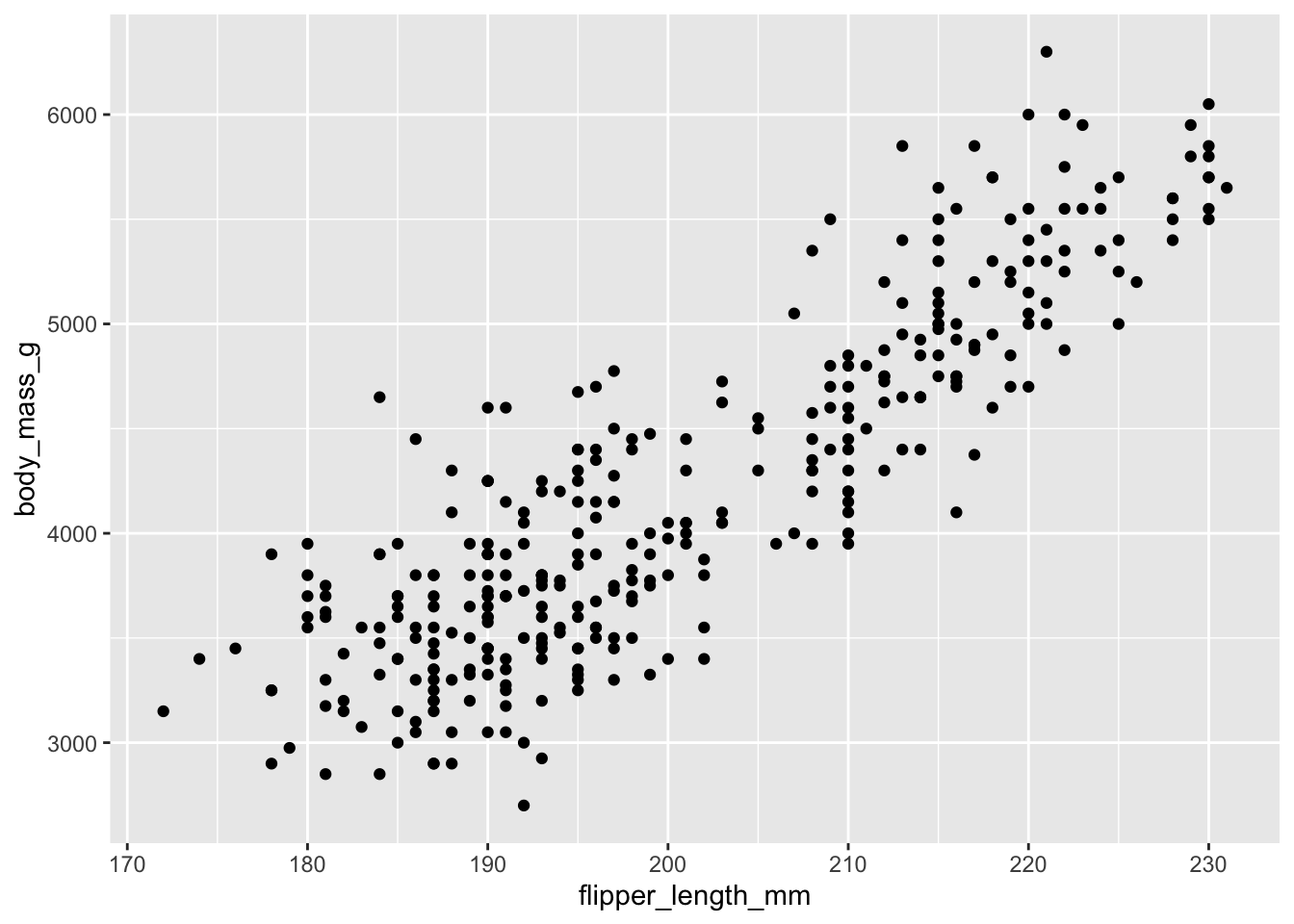

Dans ce graphique, la position en X d’un point représente sa valeur pour la variable flipper_length_mm, et en Y sa valeur pour la variable body_mass_g. Ce graphique nous permet de constater que plus les manchots ont de longues ailes (lorsque l’on se déplace vers la droite), plus ils sont lourds (on se déplace vers le haut). Lorsqu’une valeur augmente, l’autre augmente aussi.

La relation entre une variable qualitative et une quantitative

Si plutôt que d’avoir deux variables quantitatives nous voulions voir l’association entre une variable quantitative et une variable qualitative, il faudrait plutôt utiliser le diagramme à moustaches (box and whisker plot). La couche de ggplot2 pour tracer un diagramme à moustaches se nomme geom_boxplot :

ggplot(data = penguins) +
  geom_boxplot(mapping = aes(x = species, y = body_mass_g))
Warning: Removed 2 rows containing non-finite outside the scale
range (`stat_boxplot()`).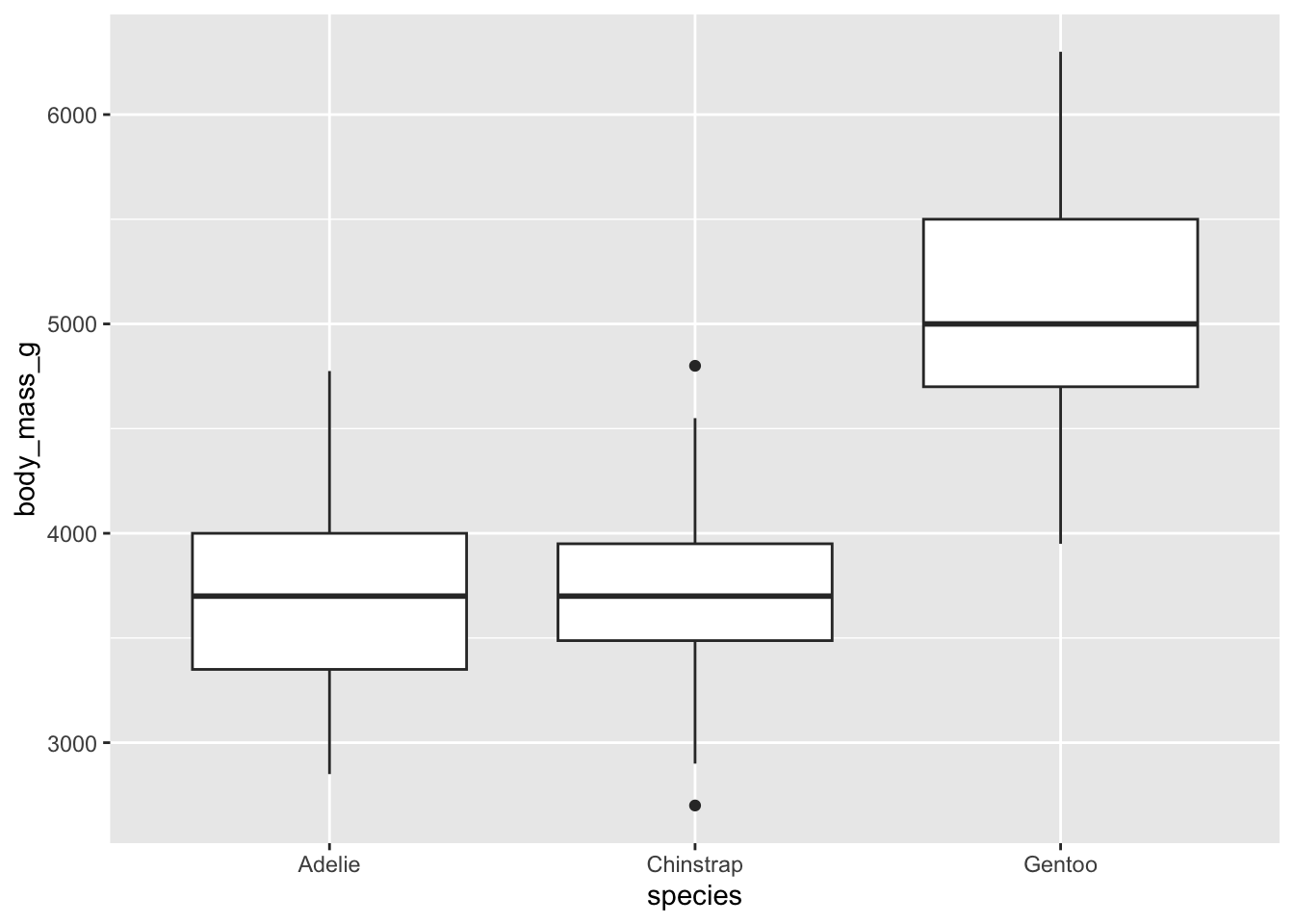

Bien qu’il soit extrêmement populaire en écologie, le diagramme à moustache est un des graphiques qui est souvent le moins bien compris et le moins standardisé. Nous prendrons donc le temps de nous y attarder un peu plus.

Remarquez d’abord qu’en X, nous avons les valeurs d’une variable qualitative (species) et en Y les valeurs d’une variable quantitative (body_mass_g). Ce que nous observons donc dans le graphique est la répartition des valeurs de poids, groupées par espèce.

De façon classique, la boîte d’un diagramme à moustache est formée par le premier et le troisième quartile. Autrement dit, la taille de la boîte nous indique entre quelles valeurs on retrouve la moitié des observations de notre variable. La ligne horizontale à l’intérieur de la boîte (souvent près du centre, mais pas nécessairement) représente la médiane des données. Elle nous indique que la moitié des valeurs sont plus grandes et la moitié plus petites que ce chiffre.

Les traits verticaux de part et d’autre de la boîte (qu’on appelle les moustaches) ne représentent pas toujours la même chose d’un logiciel à l’autre. Dans ggplot2, ils nous montrent la dernière observation qui se trouve à moins de 1,5 écart interquartile (le nom technique pour la taille de la boîte), à partir de la fin de la boîte. Cette définition n’est pas simple à comprendre, mais n’est pas si importante au bout du compte. Ce qui nous intéresse surtout, c’est de voir si au-delà des moustaches, on retrouve des points individuels. Ces points individuels (comme pour les manchots Chinstrap dans le graphique) nous indiquent des points qui n’entrent pas dans cette définition, et sont donc considérés comme des valeurs potentiellement aberrantes, qu’il vaudra la peine de vérifier et gérer correctement (nous y reviendrons).

Voici une visualisation des points à l’intérieur d’un diagramme à moustache pour vous aider à visualiser leur fonctionnement :

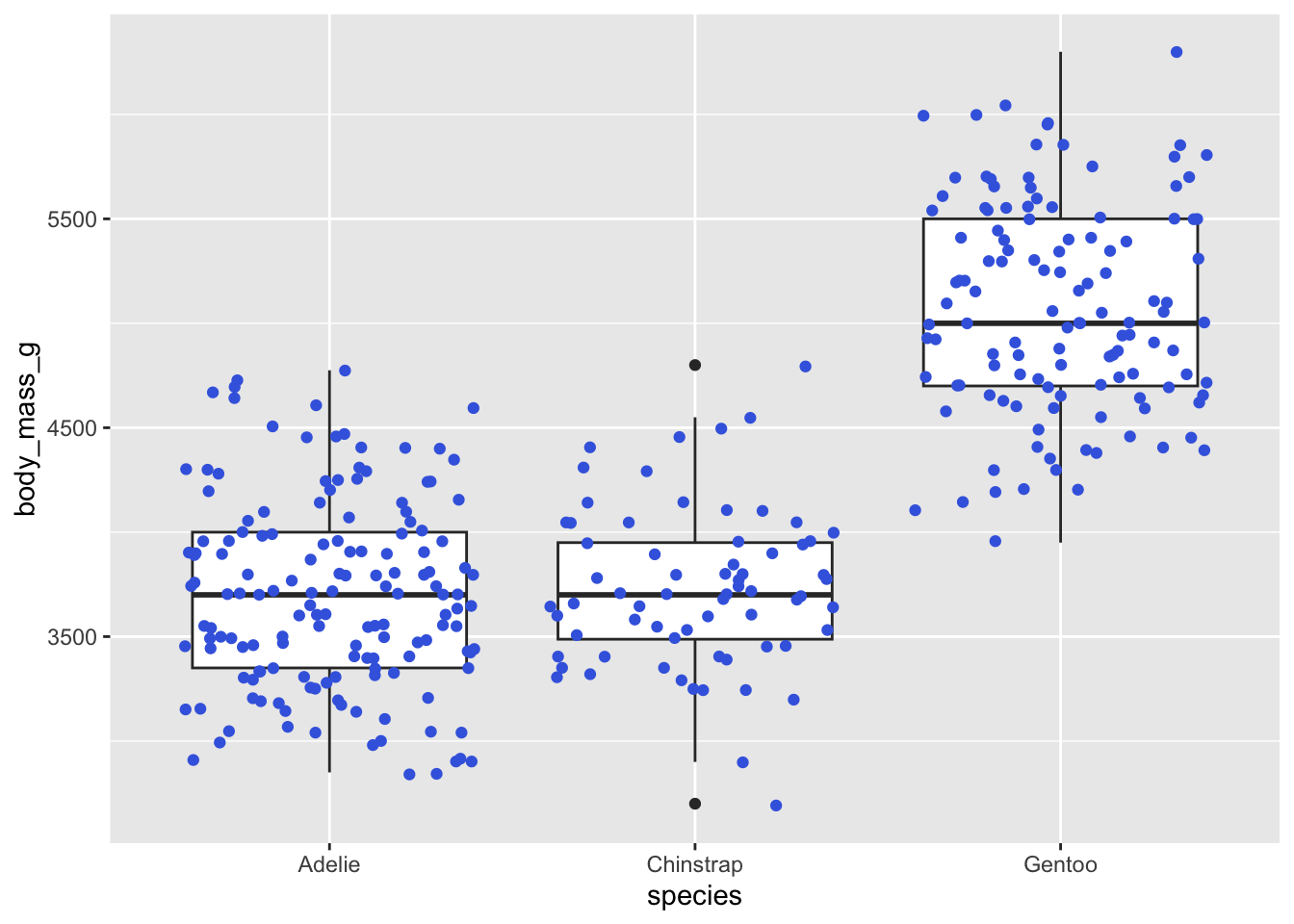
Le diagramme à moustache nous permet donc de constater que les manchots Gentoo sont plus lourds que les deux autres espèces, qui ont des poids très semblables.

Attention : vous entendrez souvent des gens discuter de leur diagramme à moustaches en parlant de moyennes, d’écart-type etc. Ces valeurs ne sont pas directement dans le graphique (sauf de rares exceptions), mais le graphique en donne quand même une bonne idée.

La relation entre deux variables qualitatives

Enfin, le dernier cas de figure à explorer est le cas où nous voulons voir si deux variables qualitatives pourraient être reliées ou associées. On pourrait par exemple se demander si le ratio mâle/femelle est différent selon les espèces de manchots.

Ce type de question est souvent exploré par un tableau de contingence, c’est-à-dire un tableau avec en X une variable qualitative, en Y une autre variable qualitative et dans chaque cellule le décompte pour chaque combinaison. Pour la question précédente, le tableau de contingence pourrait ressembler à ceci :

female male
Adelie 73 73
Chinstrap 34 34
Gentoo 58 61

En observant ce tableau, on peut constater que le ratio mâle/femelle est très proche de 50/50, et qu’il ne semble pas différer entre les espèces.

Pour les curieuses, le code pour obtenir ces chiffres sera présenté à la section Section 4.9.

On pourrait aussi observer la même information à l’aide d’un diagramme à bandes, auquel on intégrerait une composante de couleur de remplissage (fill) :

ggplot(data = penguins) +
  geom_bar(mapping = aes(x = species, fill = sex))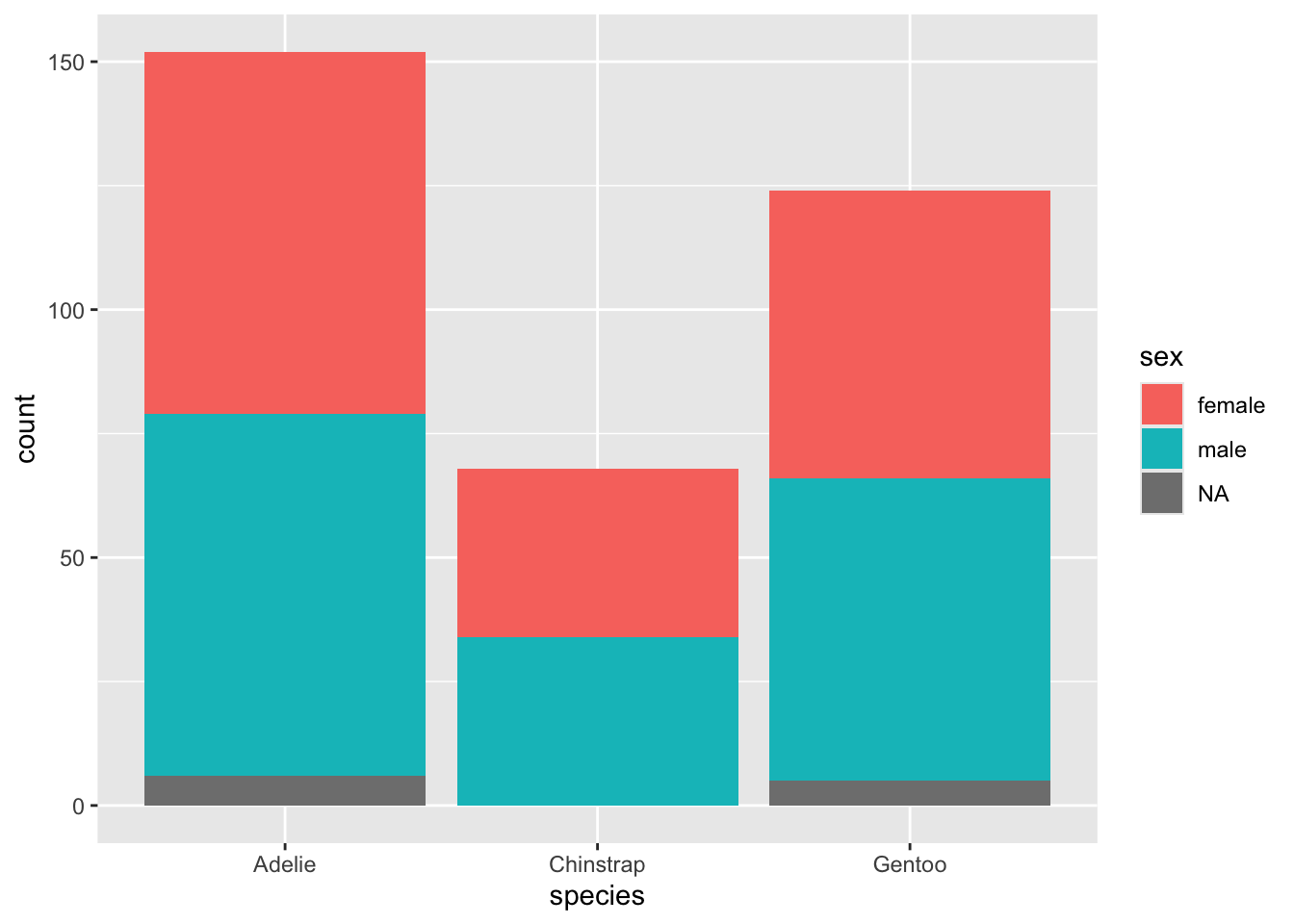

Ce graphique nous représente visuellement la même réalité : les bandes mâles et femelles sont sensiblement de la même taille pour chacune des espèces. Remarquez aussi la présence de certains individus pour lesquelles on ne connaît pas le sexe (NA)

3.8 Labo : Visualiser l’incertitude

Nous avons vu plus haut qu’un diagramme à moustaches permet de visualiser comment se comparent les valeurs d’une variable quantitative entre différents groupes.

Une autre façon d’approcher les mêmes données serait d’illustrer la moyenne et une mesure de variabilité, par exemple l’écart-type (nous y reviendrons à la Section 5.2). On utiliserait alors les fameuses barres d’erreurs.

De façon générale, les barres d’erreurs ne sont pas la façon la plus parlante d’illustrer vos données4, mais comme elles sont encore fréquemment utilisées, il est important que vous sachiez comment les utiliser.

Donc, nous allons tout d’abord se construire un petit tableau qui contiendra la moyenne et l’écart-type du poids du corps des différentes espèces de manchots de Palmer. Nous verrons en détail à la section Section 6.4 ce qui se passe dans ce petit bout de code :

library(dplyr)
pour_barres <- 
  penguins |> 
  group_by(species) |> 
  summarize (
    moyenne = mean(body_mass_g, na.rm = TRUE),
    ecart_type = sd(body_mass_g, na.rm = TRUE)
  )

pour_barres
# A tibble: 3 × 3
  species   moyenne ecart_type
  <fct>       <dbl>      <dbl>
1 Adelie      3701.       459.
2 Chinstrap   3733.       384.
3 Gentoo      5076.       504.

La façon la plus simple d’afficher des barres d’erreurs est de les ajouter à une couche de points avec la couche geom_linerange :

ggplot(data = pour_barres, mapping = aes(x = species, y = moyenne)) +
  geom_point() +
  geom_linerange(aes(
    ymin = moyenne - ecart_type, 
    ymax = moyenne + ecart_type)
  )

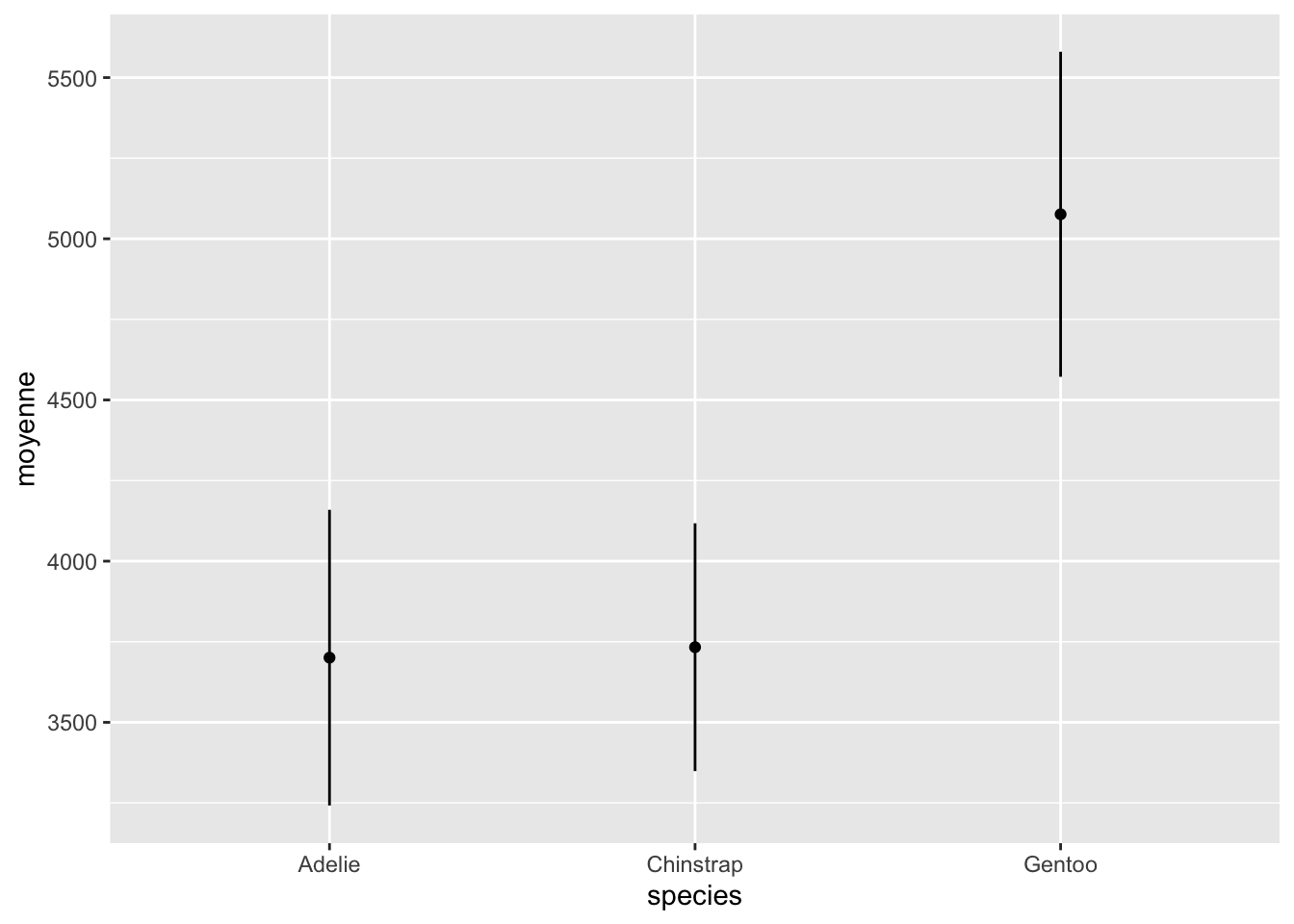
Il faut spécifier manuellement jusqu’où doit aller le haut et le bas de la barre. Ici, on a choisi un écart-type au-dessus et en-dessous de la moyenne.

Vous verrez souvent aussi des moustaches plutôt que des barres simples, que vous pouvez reproduire avec la couche geom_errorbar :

ggplot(data = pour_barres, mapping = aes(x = species, y = moyenne)) +
  geom_point() +
  geom_errorbar(aes(
    ymin = moyenne - ecart_type, 
    ymax = moyenne + ecart_type)
  )

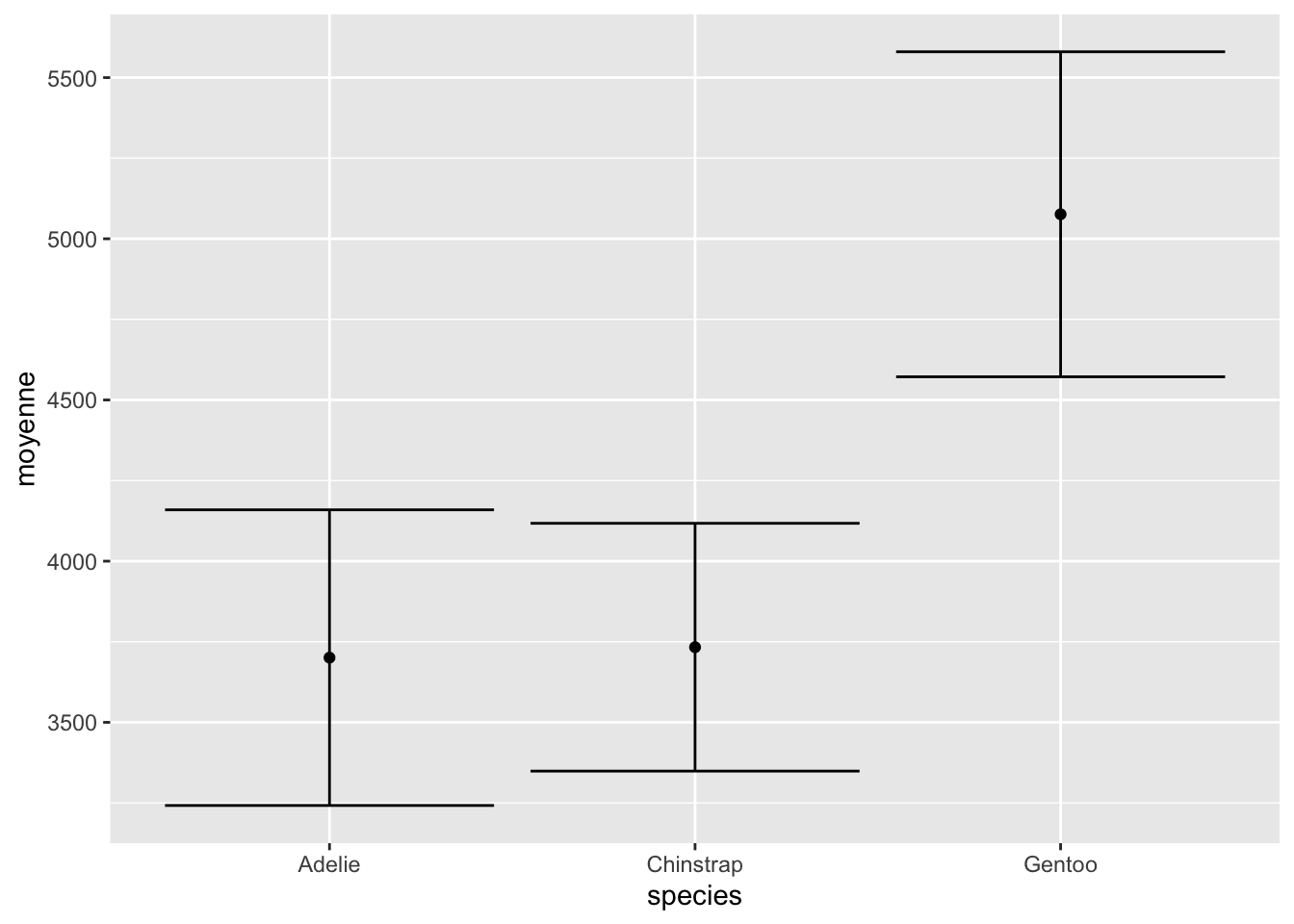
Comme la taille des moustaches est particulièrement désagréable, il peut être utile de contrôler leur largeur avec l’argument width :

ggplot(data = pour_barres, mapping = aes(x = species, y = moyenne)) +
  geom_point() +
  geom_errorbar(aes(
    ymin = moyenne - ecart_type, 
    ymax = moyenne + ecart_type),
    width = 0.2
  )

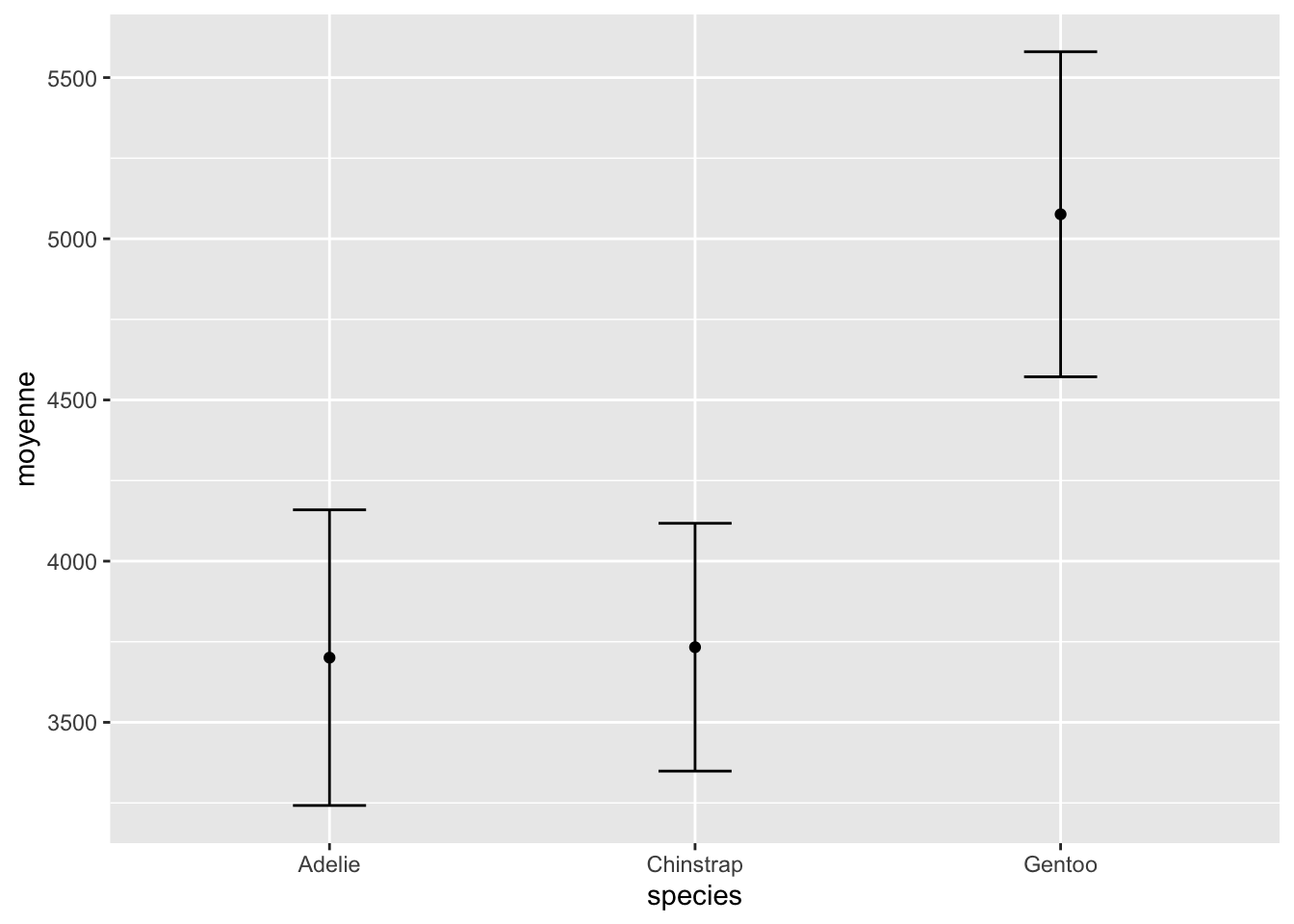
Enfin, ces barres d’erreur peuvent être ajoutées à n’importe quel type de graphique, par exemple sur un diagramme à bandes.

Bien que peu recommandés par les spécialistes en visualisation, le diagramme à bandes avec des barres d’erreurs est néanmoins très utilisé, entre autres en biologie médicale.

ggplot(data = pour_barres, mapping = aes(x = species, y = moyenne)) +
  geom_col() +
  geom_errorbar(aes(
    ymin = moyenne - ecart_type, 
    ymax = moyenne + ecart_type),
    width = 0.2
  )

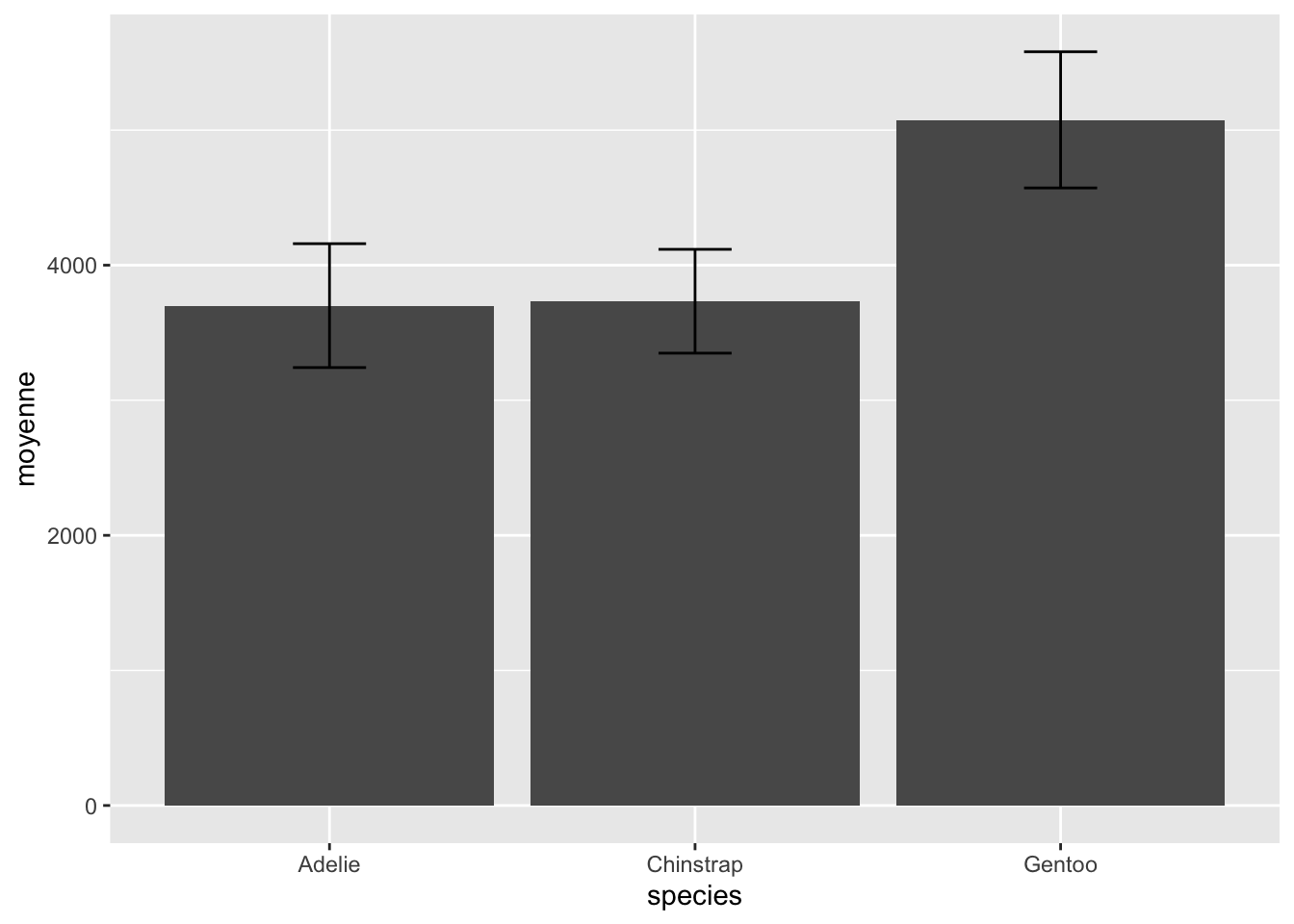
Remarquez que dans ce cas, il faut utiliser un geom_col puisque nos valeurs sont déjà pré-calculées.

Important

Bien que tous les exemples ci-haut aient utilisé l’écart-type comme mesure d’erreur, les barres d’erreur peuvent être utilisées pour illustrer plusieurs choses différentes. Entre autres :

  • L’écart-type
  • L’erreur-type
  • 2 x l’écart-type
  • L’intervalle de confiance

Soyez très attentives à bien communiquer ce que représentent vos barres d’erreurs et assurez-vous de bien comprendre ce qu’elles représentent dans vos lectures, car elles peuvent varier d’un auteur à l’autre…

3.9 Exercices

En vous inspirant de la Section 3.6, créez un graphique avec en X la longueur du bec (bill_length_mm) et en Y la profondeur du bec (bill_depth_mm). Remplacez les points par des carrés. La couleur de chaque carré devra correspondre à l’île où a été mesuré l’individu (island). Comment sont reliées ces deux variables?

En adaptant le bon exemple dans la section Section 3.7, affichez un diagramme à moustaches présentant la distribution des longueurs d’aile (flipper_length_mm) pour chacune des espèces. Une fois ce graphique réussi, adaptez-le pour que chaque espèce possède sa propre couleur de remplissage dans le diagramme. Quelle espèces possède les ailes les plus longues?

Enfin, en prenant exemple sur la section Section 3.8, créez un graphique montrant la moyenne et l’écart-type de la longueur des ailes (flipper_length_mm). Comme on peut utiliser plusieurs couches différentes pour afficher cette information, reprenez ensuite ce même graphique, mais avec une couche différente. Quelle est votre façon préférée d’afficher cette information?

3.10 En résumé

Donc, si on résume comment choisir le bon graphique selon ce que l’on veut explorer, nous avons vu :

  • Distribution des valeurs d’une seule variable :
    • Quantitative : Histogramme de fréquences
    • Qualitative : Diagramme à bandes
  • Relation ou association entre deux variables :
    • Quantitative + Quantitative = Nuage de points
    • Quantitative + Qualitative = Diagramme à moustaches
    • Qualitative + Qualitative = Tableau de contingence OU diagramme à bande avec couleur de remplissage.

  1. https://fr.wikipedia.org/wiki/Rouge_vert_bleu↩︎

  2. https://sape.inf.usi.ch/quick-reference/ggplot2/colour↩︎

  3. http://www.sthda.com/english/wiki/ggplot2-point-shapes#point-shapes-in-r↩︎

  4. https://gorelik.net/2019/10/07/error-bars-in-bar-charts-you-probably-shouldnt/↩︎