13 Tests de comparaison de deux moyennes
Il existe plusieurs façons différentes de comparer la moyenne de deux échantillons pour savoir si ceux-ci proviennent de populations ayant des moyennes différentes. Nous en verrons deux dans ce chapitre, soit le test de T de Welch pour variance inégales et le test de T pairé.
13.1 Parenthèse historique
Si vous consultez d’anciennes versions de ce livre, ou même plusieurs manuels classiques de biostatistiques, vous constaterez probablement qu’il existe un troisième test de T : le test de T pour variances égales. Puisque son calcul était plus simple à effectuer manuellement, il était souvent considéré comme LE test à effectuer pour comparer la moyenne de deux groupes.
Cependant, comme son nom l’indique, ce test comportait une assomption supplémentaire, soit l’égalité des variances entre les deux échantillons. Il a donc longtemps été recommandé d’effectuer l’opération en deux étapes, soit un test d’égalité des variances, suivi du test de T suggéré par le test d’égalité des variances (égales ou non). Il est cependant maintenant reconnu que cette procédure (1) est inutile puisque le test de T de Welch possède essentiellement la même puissance statistique que le test de T pour variance égales et (2) augmente le taux d’erreur de type I, puisque l’on enchaîne deux tests un derrière l’autre plutôt que d’en effectuer un seul.
Conformément à la recommandation moderne (p. ex. Ruxton (2006) et Hayes et Cai (2007)), je propose maintenant d’appliquer directement le test de Welch, sans passer par la procédure en deux étapes. En plus, tout le monde y gagne, car cela faciletera aussi beaucoup votre travail!
13.2 Le test de T de Welch
Le test de T de Welch s’utilise pour comparer la moyenne de deux échantillons pour savoir si elles sont significativement différentes. On pourrait par exemple l’utiliser pour savoir si les oiseaux en milieu urbain sont en moyenne plus gros que les oiseaux en milieu naturel. On pourrait par par exemple avoir capturé 20 oiseaux en milieu urbain et mesuré leur poids, puis 40 en milieu naturel et aussi mesuré leur poids.
Étape 1 : Définir les hypothèses
Les hypothèses statistiques du test de T de Welch sont pour l’hypothèse nulle (H0) que les moyennes sont égales entre les groupes et l’hypothèse alternative (H1) est qu’il existe une différence de moyenne entre les deux groupes.
Pour notre exemple sur les oiseaux, nos hypothèses statistiques seraient donc les suivantes : \[ \begin{aligned} H_0 : \mu_{urbain} = \mu_{naturel}\\ H_1 : \mu_{urbain} \ne \mu_{naturel} \end{aligned} \]
Étape 2 : Explorer visuellement les données
Le test de T de Welch comporte deux assomptions importantes. La première est que les observations sont indépendantes les unes des autres. Un cas classique où cette assomption ne serait PAS respectée serait si vous avez mesuré les mêmes individus à deux dates différentes et vous voudriez savoir si leur poids a diminué ou non. Dans ce cas, les observations ne sont pas indépendantes, puisque le même individu est mesuré plusieurs fois. Il faudrait alors appliquer le test de T pairé (voir Section 13.4).
La deuxième assomption du test de T de Welch est que l’échantillon provienne d’une distribution normale, ou sinon, que l’échantillon soit relativement grand, pour pouvoir s’appuyer sur the théorème central limite
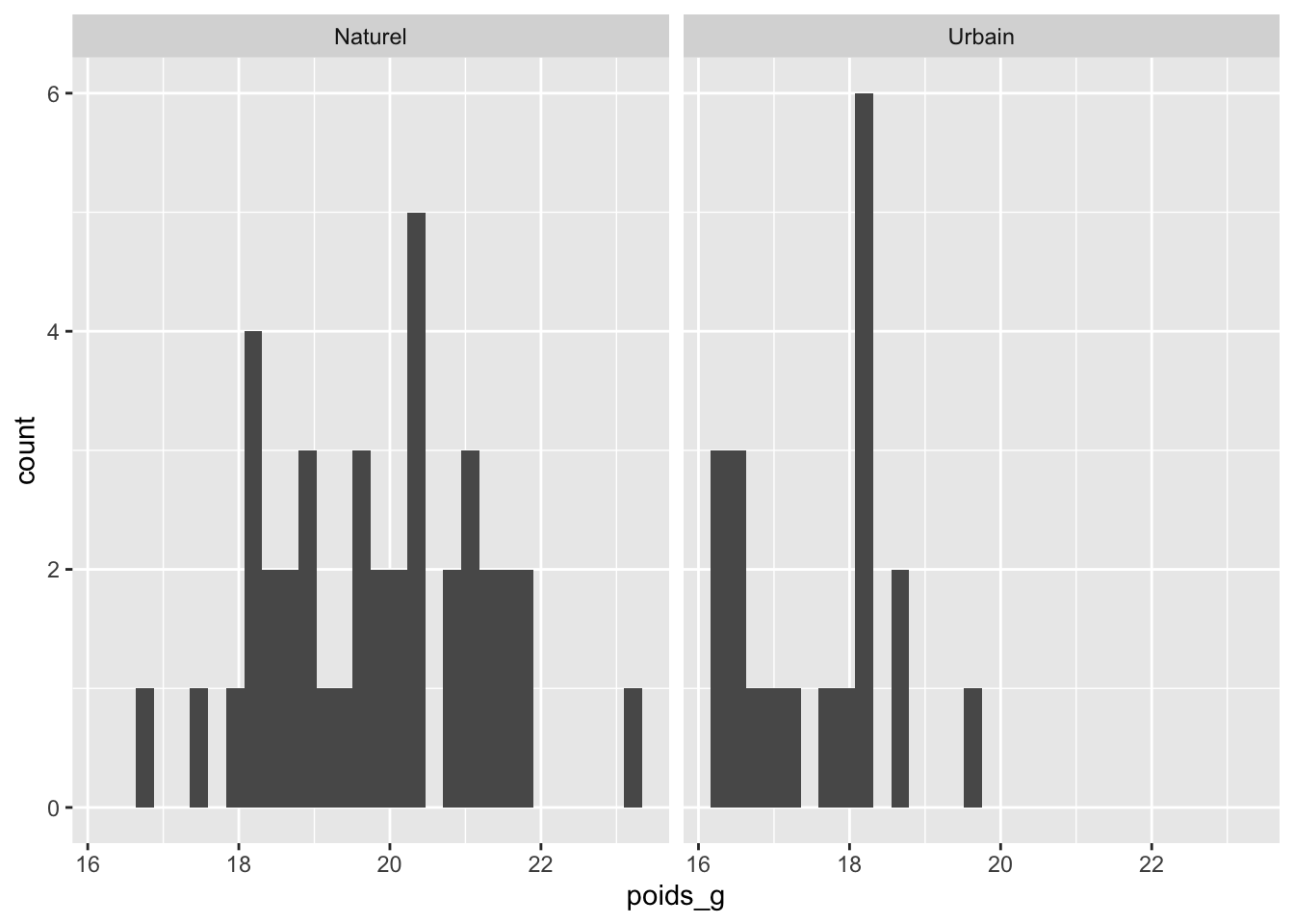
On peut donc se contenter d’une exploration visuelle de nos deux groupes à l’aide d’un histogramme, comme ceci :
Enfin, une fois les assomptions vérifiées, il importe aussi d’aller voir à quoi ressemble la moyenne des deux échantillons, pour se faire une idée avant de commencer, si l’on pense trouver une différence moyenne ou non entre les groupes. La façon idéale d’inspecter une différence de moyenne entre deux groupes et de tracer un diagramme à moustaches de ces données :
Au premier coup d’oeil, on voit une différence de près de 2 g entre nos deux groupes, et cette différence paraît assez claire par rapport à la variabilité pour être statistiquement significative.
Étape 3 : Calculer la statistique de test
Je vous inscris ici les formules pour que vous les ayez sous la main si vous en avez besoin un jour, mais vous n’aurez probablement jamais besoin de les calculer manuellement :
\[ T = \frac{\bar{x_1}-\bar{x_2}} {\sqrt{ \frac{s^2_1}{n_1} + \frac{s^2_2}{n_2} }} \]
Où ni est le nombre d’observations, xi la moyenne de l’échantillon i, s2i est l’estimé de variance de chacun des groupes et ni la taille de l’échantillon de chacun des groupes. Autrememnt dit, la différence entre les moyennes, divisée par l’erreur type de la différence entre les deux moyennes.
Il existe une règle mathématique qui dit que, si l’on soustrait deux distributions normales, la variance de cette différence sera la somme des deux variances originales. Ici, puisque nous voulons l’erreur-type, il faut ensuite appliquée la racine carrée…
L’important est surtout de comprendre que plus la différence entre les moyennes sera grande, plus la valeur de T sera grande aussi (en valeur absolue). À l’inverse, plus la variabilité des données sera grande, plus la statistique de T sera près de zéro. Les deux ingrédients pour trouver un test de T significatif sont donc une grande différence de moyenne entre les groupes et une petite variabilité entre les individus.
Pour notre exemple, x1 est 19.81 g et x2 est 17.55 g. La taille de nos échantillons n1 et n2 est respectivement de 40 et 20 individus et la variance de chaque groupe était de 1.93 g2 et de 1.04 g2. La valeur de notre statistique de T est donc de 7.14.
Étape 4 : Obtenir la valeur de p
Comme pour le test de T à un échantillon (voir Chapitre 12), la statistique de T calculée ici suit une distribution de T, mais le calcul des degrés de liberté est un peu plus complexe (!) :
\[\nu \approx \frac{\left(\frac{s_1^2}{N_1} + \frac{s_2^2}{N_2}\right)^2} {\frac{s_1^4}{N_1^2 \nu_1} + \frac{s_2^4}{N_2^2 \nu_2}}\]
Comme la formule l’indique, il s’agit d’une approximation, puisque le test combine les deux variances après les avoir divisées par la taille des échantillons, ce qui revient à donner plus de poids au groupe le plus précis.
Pour notre exemple, les degrés de liberté sont donc de 49.81 et la valeur de p est de 0.0000000037.
Étape 5 : Rejeter ou non l’hypothèse nulle
Nous pouvons maintenant prendre notre décision statistique. Puisqu’une telle valeur de statistique de T est très rarement observée dans de telles circonstances si les moyennes des populations étaient égales (0.0000000037 est vraiment plus petit que 0,05), alors on peut rejeter notre hypothèse nulle d’aucune différence de moyenne entre les populations. Les moyennes des deux groupes sont significativement différentes.
Étape 6 : Citer la magnitude de l’effet et son intervalle de confiance
Je vous le rappelle encore une fois, il est très important, après avoir déterminé si notre test est significatif ou non de rapporter la magnitude de l’effet trouvé (ici la différence entre les deux moyennes) et son intervalle de confiance.
Notre magnitude d’effet est une simple soustraction des deux moyennes, soit 19.81 g - 17.55 g = 2.26 g.
L’intervalle de confiance de cette différence de moyenne quant à lui se calcule à l’aide de la différence, de l’erreur-type de la différence et d’une valeur extraite de la distribution de T, soit :
\[ IC(\mu_1-\mu_2): \overline{X}_1 - \overline{X}_2 \pm \sqrt{ {s_{\bar{X}_1}^2} + {s_{\bar{X}_2}^2} } \times t_{\nu, 1-\alpha/2}\]
Encore une fois, vous n’aurez pas à calculer manuellement cet intervalle de confiance, mais comprenez que plus l’erreur-type sera grand, plus l’intervalle de confiance sera large.
Dans un rapport, vous pourriez écrire ce résultat comme ceci :
«Les oiseaux présentaient une différence significative de poids entre les milieux naturels et urbains (Test de Welch, T49.81 = 7.14, p = 0.0000000037) L’intervalle de confiance de cette différence se situait entre 1.62 et 2.89 g supplémentaires chez les oiseaux de milieu naturel (IC 95 %).»
13.3 Labo : Le test de T de Welch
Pour ce laboratoire, nous tenterons de répondre à la question : est-ce que le relief de l’habitat affecte la taille des ailes chez les manchots Adélie. Pour les besoins de l’expérience, nous assumerons que les îles Torgersen et Biscoe ont des reliefs très différents, nous permettant de tester notre hypothèse.
Étape 1 :
\[ \begin{aligned} H_0 = \mu_{Torgersen} = \mu_{Biscoe}\\ H_1 = \mu_{Torgersen} \ne \mu_{Biscoe} \end{aligned} \]
Étape 2 :
Nous commencerons par activer les librairies nécessaires et préparer deux mini-tableaux de données contenant uniquement les observations nécessaires pour appliquer notre test :
library(tidyverse)
library(palmerpenguins)
Attaching package: 'palmerpenguins'The following objects are masked from 'package:datasets':
penguins, penguins_rawadelie <-
penguins |>
filter(species == "Adelie") |>
filter(island %in% c("Torgersen", "Biscoe")) |>
drop_na(flipper_length_mm)
torgersen <- adelie |> filter(island == "Torgersen")
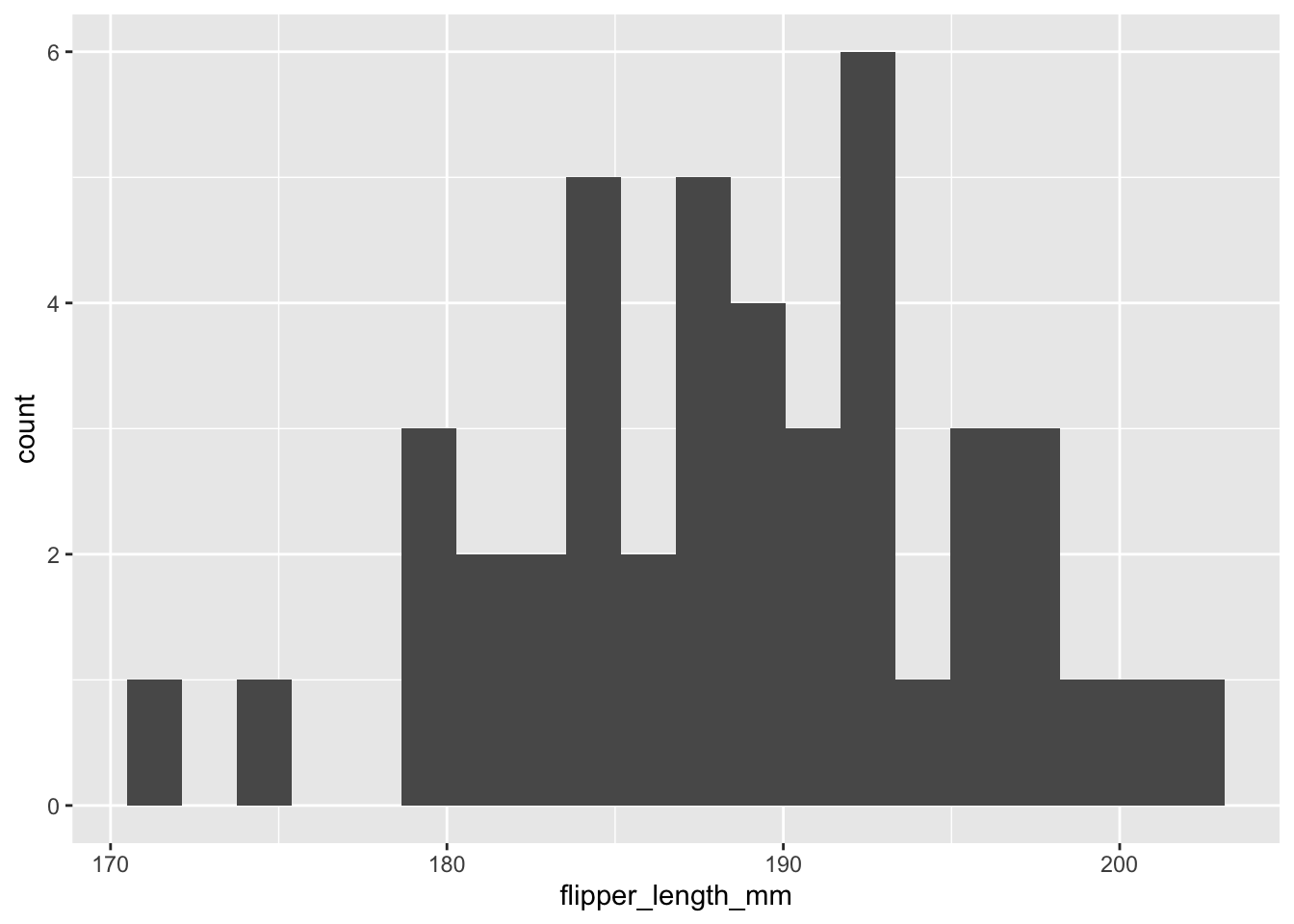
biscoe <- adelie |> filter(island == "Biscoe")Il faut ensuite valider visuellement nos données et leurs distributions.
biscoe |>
ggplot() +
geom_histogram(aes(x = flipper_length_mm), bins = 20)
torgersen |>
ggplot() +
geom_histogram(aes(x = flipper_length_mm), bins = 20)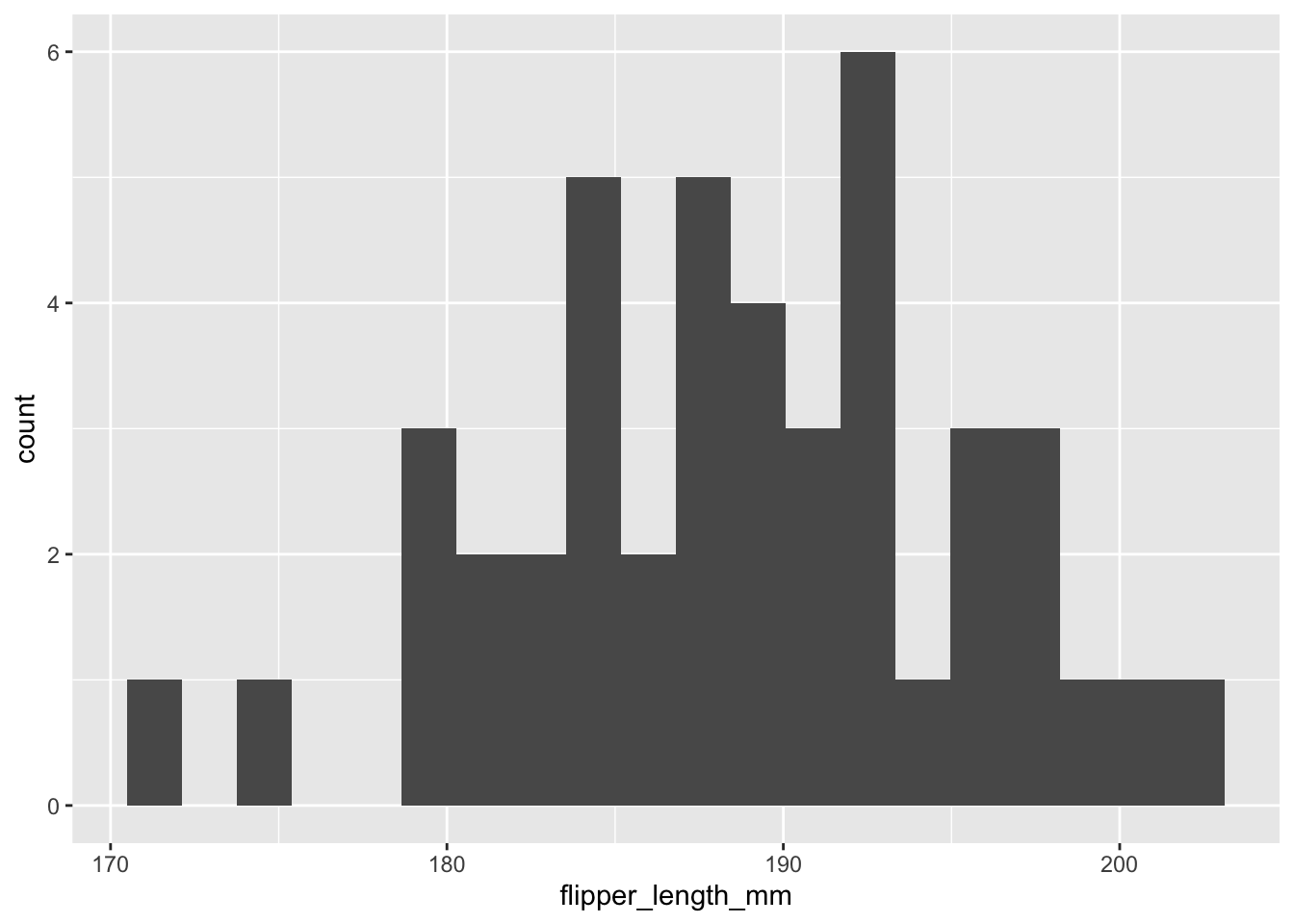
À première vue, les distributions sont suffisamment normales pour appliquer un test de Welch.
adelie |>
ggplot(aes(island, flipper_length_mm)) +
geom_boxplot()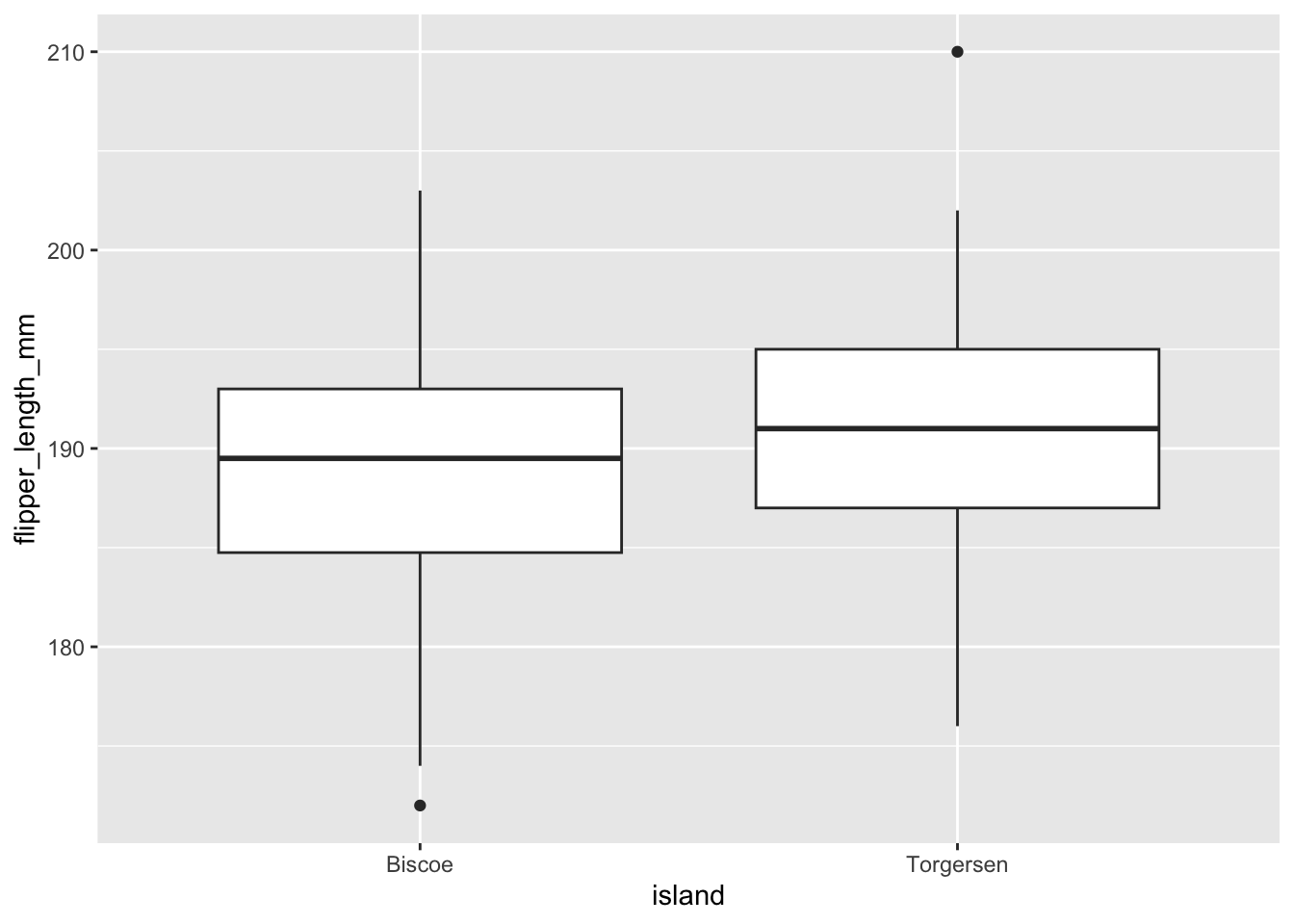
Visuellement, la taille des ailes de manchots sur Torgersen est légèrement plus grande, mais elle ne se distingue pas particulièrement.
Étapes 3 et 4
La fonction pour effectuer le test de Welch est la même que le test de T à un échantillon, mais cette fois-ci, il faut lui fournir deux échantillons (eh oui!).
Par défaut, si on ne mentionne rien, la fonction applique un test de Welch (i.e. pour variances différentes). Si vous voulez absolument effectuer un test pour variances égales, vous devrez ajouter l’argument var.equal = TRUE.
t.test(torgersen$flipper_length_mm, biscoe$flipper_length_mm)
Welch Two Sample t-test
data: torgersen$flipper_length_mm and biscoe$flipper_length_mm
t = 1.7939, df = 88.506, p-value = 0.07624
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-0.2585247 5.0597724
sample estimates:
mean of x mean of y
191.1961 188.7955 La première ligne nous informe d’abord de quel test a été utilisé. Comme la fonction t.test peut être utilisée pour plusieurs tests différents selon les arguments utilisés, vous comprenez maintenant l’utilité de cette première ligne. La ligne suivante nous rappelle les données utilisées pour le test. La troisième nous fournit la statistique de test (T) ainsi que ses degrés de liberté (df) et la valeur de p associée (ici p=0,076). La ligne suivante nous rappelle quelle est l’hypothèse alternative du test de Welch. Ensuite, R nous fournit l’intervalle de confiance de la différence de moyenne entre nos deux groupes, soit de -0,26 à 5,06. Autrement dit, l’intervalle de confiance de la différence n’exclut pas la valeur de zéro. Enfin, la dernière ligne nous donne la moyenne de chacun de nos groupes.
Étape 5 :
Comme la valeur de p est plus grande que le seuil de signification (0,076 vs 0,05), notre résultat n’est pas significatif. Il est relativement commun de trouver une telle différence lorsque les moyennes des deux populations sont égales
Étape 6 :
Nous aurions donc pu écrire ce résultat comme ceci : « Il n’y a pas de différence significative dans la taille des ailes des manchots Adélie entre les îles Torgersen et Biscoe (Test de Welch, T88,5 = 1,79, p = 0,076). L’intervalle de confiance à 95% de la différence entre les deux îles allait de -0,26 à +5,06 mm. ».
13.4 Le test de T pairé
Comme son nom le suggère, le test de T pairé est utilisé lorsque notre expérience est structurée de manière à ce que chacune des mesures dans le premier échantillon corresponde à une mesure dans le deuxième échantillon. Vous verrez aussi parfois le terme “données appariées”, ce qui est équivalent.
Ce test est approprié, par exemple, lorsque l’on fait un suivi du poids des individus dans une population, la mesure de départ de chaque individu étant le premier échantillon et la mesure finale devenant le deuxième échantillon. Il peut être aussi utile pour évaluer le résultat d’une expérience où l’on veut voir si un traitement a fonctionné ou non. On pourrait par exemple avoir mesuré le nombre d’insectes sur une série de plantes (n=22), avoir appliqué un traitement insecticide, et vérifié une semaine plus tard le nombre d’insectes présents sur chacune des plantes.
On peut donc s’imaginer, pour chacune des plantes son évolution en nombre d’insectes avant et après le traitement, un peu comme ceci :
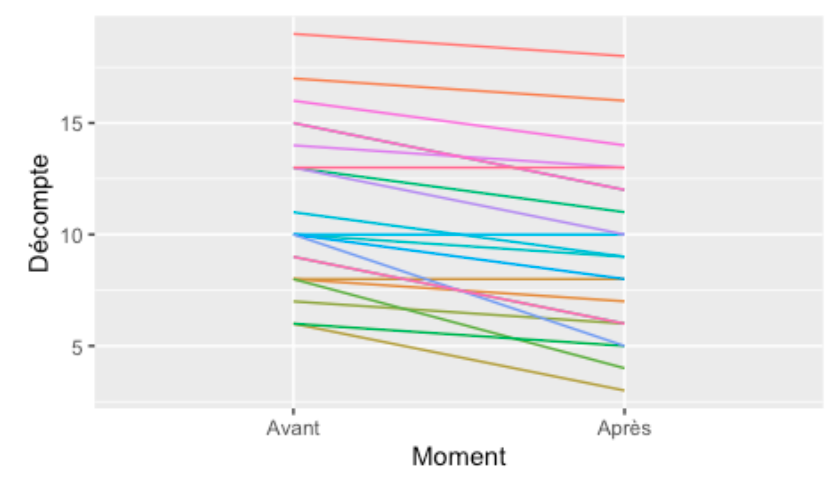
Par contre, au moment de calculer le test, on ne s’intéresse pas directement aux valeurs mesurées avant ou après, mais plutôt à la différence entre les deux moments pour chacune des plantes. On aurait donc des valeurs comme -1, 0, -3, +1, etc. pour la différence de nombre d’insectes avant et après. Le test de T pairé regarde si la moyenne de ces différences est différente de zéro ou non. Il faut donc plutôt s’imaginer un graphique comme celui-ci lors que l’on réfléchit au test de T pairé :
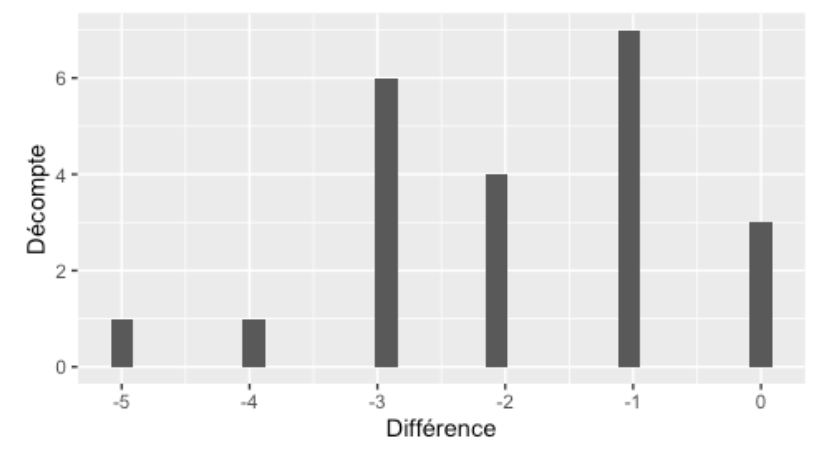
On effectue donc essentiellement un test de T à un échantillon basé sur la différence avant-après.
Voyons comment appliquer ce test en se basant sur notre exemple d’insecticide.
Étape 1 : Définir les hypothèses
Comme le test de T pairé s’intéresse à la différence entre le premier et le deuxième échantillon (en pairant les données…), les hypothèses sont aussi structurées de cette façon.
L’hypothèse nulle étant que la différence moyenne est de zéro, et l’hypothèse alternative étant que cette différence est différente de zéro : \[ \begin{aligned} H_0 : \mu_0 = 0\\ H_1 : \mu_0 \ne 0 \end{aligned} \]
On utilise ici une valeur de référence de zéro par simplicité, mais notez qu’il est souvent plus intéressant d’utiliser une valeur différente, basée sur votre connaissance scientifique du phénomène à l’étude. Si on avait trouvé une étude qui disait qu’il fallait diminuer d’au moins 10 insectes par plante pour avoir un effet sur sa croissance, il aurait été beaucoup plus intéressant d’utiliser cette valeur comme référence plutôt que zéro. On aurait donc testé si l’insecticide diminue suffisamment le nombre d’insectes pour affecter la croissance de la plante.
Étape 2 : Explorer visuellement les données
La principale assomption du test de T pairé est que la distribution des différences suit une distribution normale. Il faut donc tracer l’histogramme de cette différence pour avoir une idée de la forme de la distribution. Comme nous avons tracé ce graphique à la section précédente, nous ne le retracerons pas ici. En observant rapidement le graphique, on réalise que la moyenne des différences semble bien différente de zéro. On devrait s’attendre à trouver un effet significatif du traitement insecticide, qui ferait diminuer le nombre d’insectes sur les plantes.
Étape 3 : Calculer la statistique de test
Le calcul de la statistique de test est identique à celui du test de T à un échantillon (voir Chapitre 12). Ici la moyenne des différences est de -1,91 insectes, l’écart type est de 1,34 et n=22, donc la statistique de T sera de 6,686 insectes.
Étape 4 : Obtenir la valeur de p Comme pour le test de T à un échantillon, la distribution de la statistique de T devrait suivre une distribution de T de Student avec n-1 degrés de liberté. C’est donc dans cette distribution qu’il faut aller déterminer la valeur de p. Dans notre cas, p= 0,00000012.
Étape 5 : Rejeter ou non l’hypothèse nulle
Comme observer une telle différence est très rare lorsque l’on échantillonne des données telles que stipulées avec l’hypothèse nulle (0,00000012 est vraiment plus petit que 0,05), on rejette l’hypothèse nulle d’une différence de zéro. On peut donc dire que l’insecticide a un effet significatif sur le nombre d’insectes.
Étape 6 : Citer la magnitude de l’effet et son intervalle de confiance.
Pour le test de T pairé, la magnitude de l’effet est l’ampleur de la différence entre nos deux échantillons. Ici, nous avons calculé que cette différence est en moyenne de -1,91 insectes. Avec le même calcul que pour le test de T à un échantillon, on peut calculer l’intervalle de confiance à 95 % de cette différence, qui se situera entre -2,50 et -1,31 insectes.
On peut enfin écrire notre résultat comme ceci : « L’effet moyen de l’insecticide était de -1,91 insecte par plante ± 0,59 (I.C. 95 %), ce qui en fait une différence significativement différente de zéro (t22 = 36,686, p = 0,00000012). »
13.5 Labo : Le test de T pairé
Puisque le tableau de données penguins ne contient pas de données pairées, nous allons devoir, pour cet exemple, se créer un petit tableau permettant d’étudier le gain de poids d’une espèce de bruant à la fin de l’été en préparation pour la migration. Notre question écologique étant de savoir si les bruants prennent effectivement du poids avant la migration ou non.
Nous allons donc activer nos librairies, puis créer manuellement notre tableau de données, à l’aide du code suivant :
engraissement <- data.frame(
poids_debut_g = c(7.1, 3.0, 6.0, 4.0, 4.2),
poids_fin_g = c(8.2, 3.5, 5.6, 4.5, 6.1)
) |>
mutate(difference = poids_fin_g - poids_debut_g)
engraissement poids_debut_g poids_fin_g difference
1 7.1 8.2 1.1
2 3.0 3.5 0.5
3 6.0 5.6 -0.4
4 4.0 4.5 0.5
5 4.2 6.1 1.9Remarquez que dans la même étape où nous créons notre tableau de données, nous créons immédiatement une colonne de différence. Cela facilitera notre travail plus tard.
Étape 1 : \[ \begin{aligned} H_0 : \mu_{preparation} = 0 \\ H_1 : \mu_{preparation} \ne 0 \end{aligned} \]
Autrement dit, est-ce que la moyenne de gain de poids durant la préparation à la migration est différente de zéro.
Étape 2 :
Pour le test de T pairé, on peut en un seul graphique valider l’assomption de normalité de la différence, et aussi visualiser la magnitude de l’effet. Pour se faire, nous créons un histogramme, auquel nous ajoutons une couche de ligne verticale, permettant de voir la valeur de référence (dans notre cas, zéro) :
engraissement |>
ggplot(aes(x = difference)) +
geom_histogram() +
geom_vline(xintercept = 0, color = "blue", linetype = "dashed")`stat_bin()` using `bins = 30`. Pick better value with
`binwidth`.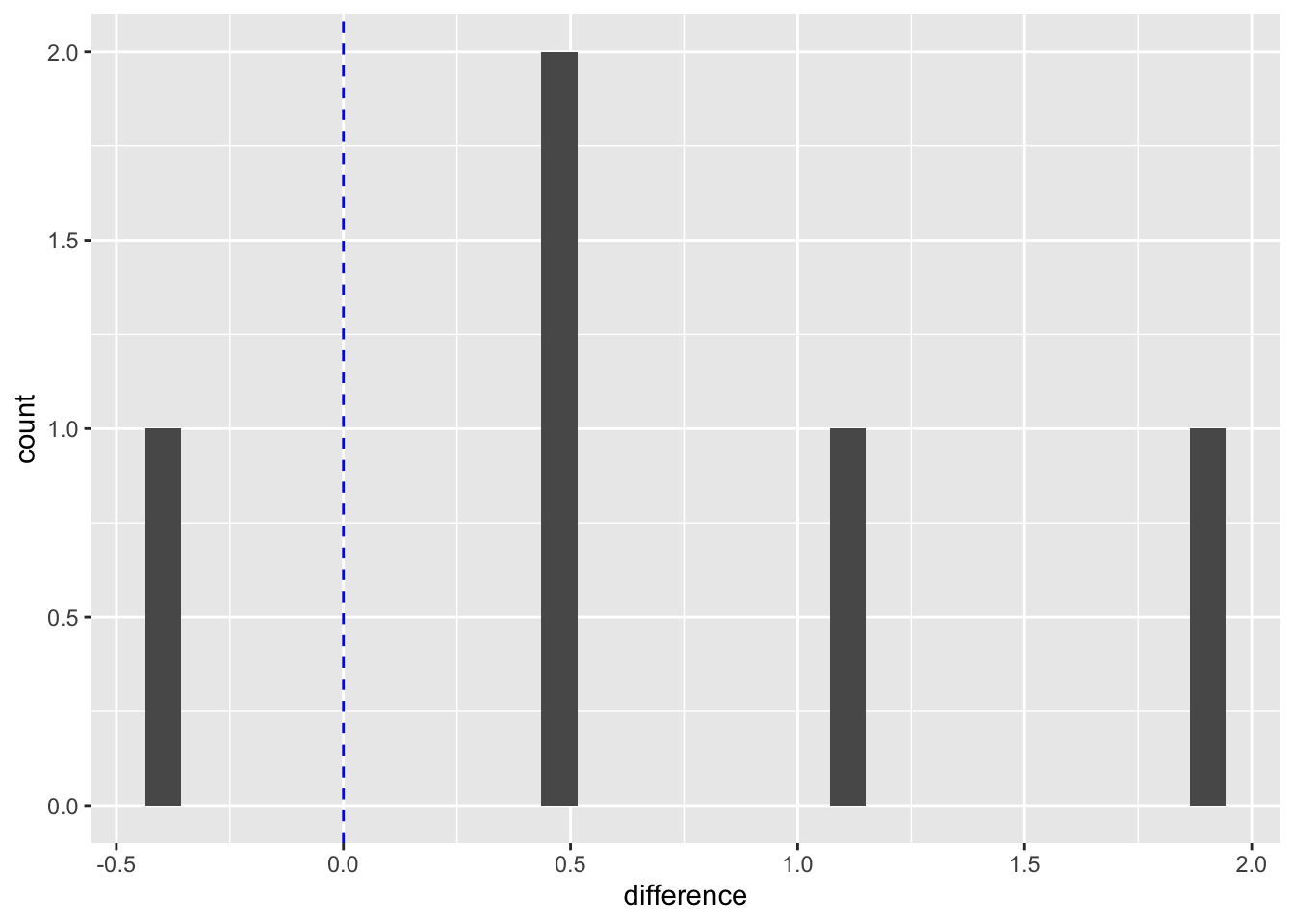
On peut donc constater d’un seul coup d’oeil que nos données semblent normales (pour le peu que l’on en a) et que le poids des bruants, à une exception près, semble avoir augmenté durant la période étudiée.
Étapes 3 et 4 :
Pour calculer le test de T pairé dans R, on utilise la fonction t.test exactement comme pour le test de T à un échantillon :
t.test(engraissement$difference)
One Sample t-test
data: engraissement$difference
t = 1.8947, df = 4, p-value = 0.131
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
-0.3350491 1.7750491
sample estimates:
mean of x
0.72 R nous mentionne qu’il a effectué un test de T à un échantillon. C’est correct, c’est ce que nous voulions. Il nous fournit ensuite les mêmes informations qu’au Chapitre 12, mais c’est à nous de les interpréter comme étant la moyenne des différences. Le test nous informe donc que la moyenne des différences de poids pendant la préparation à la migration est de 0,72 g.
Étape 5 :
La sortie de R nous informe aussi que cette différence n’est pas significative au seuil de 0,05 (p=0,131). Il important de nuancer ici le fait que bien l’on trouve une différence claire dans nos données, notre taille d’échantillon est tellement faible (n=5) qu’il serait à peu près impossible de trouver une valeur de p significative comme tel : nous manquons clairement de puissance statistique.
Étape 6 : Nous pourrions donc écrire ce résultat comme ceci : « Le gain de poids moyen des bruants en préparation de la migration était en moyenne de 0,72 g ± 1,06 (I.C. 95 %). Cette différence n’était pas significativement différente de zéro (t4=1,894, p = 0,131 ) »
Notez qu’il existe aussi une façon de calculer le test de T pairé sans calculer à l’avance une colonne de différence. Il faut à ce moment passer les deux colonnes à la fonction t.test et lui mentionner de nous calculer un test pairé :
t.test(engraissement$poids_debut_g, engraissement$poids_fin_g, paired = TRUE)On obtient alors exactement le même résultat :
Paired t-test
data: engraissement$poids_debut_g and engraissement$poids_fin_g
t = -1.8947, df = 4, p-value = 0.131
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-1.7750491 0.3350491
sample estimates:
mean difference
-0.72 13.6 Récapitulatif
Si on fait un petit récapitulatif des tests vus jusqu’à présent, vous êtes maintenant en mesure de gérer les situations suivantes :
- Pour comparer une moyenne à une valeur cible : Test de T à un échantillon
- Pour comparer deux moyennes entre-elles : Test de Welch
- Pour comparer la moyenne de données pairées : Test de T pairé.