12 Initiation aux tests statistiques

12.1 À quoi servent les tests statistiques

Nous avons parlé au début de ce livre du fait que la nature est intrinsèquement variable. Il devient donc difficile de savoir si ce que nous observons est représentatif ou s’il s’agit de bizarreries dues au hasard pour cet échantillon en particulier. Les tests statistiques nous servent à mettre un chiffre sur cette incertitude. Vous apprendrez dans ce chapitre que l’on considère comme statistiquement significatif tout constat qui a moins de 5 % de chance d’être observable par le fruit du hasard seulement.

12.2 Mettre l’emphase sur ce qui est important

Le monde des sciences accorde souvent une grande importance au fait que notre résultat soit statistiquement significatif ou non. Il ne faut cependant jamais perdre de vue que le fait que notre résultat soit significatif ou non ne nous informe pas quant à l’ampleur du phénomène observé. Le chiffre qui nous renseigne sur cette ampleur ce nomme plutôt la taille de l’effet.

Si p. ex. on discute de l’apport nutritif d’une proie ingérée par un hibou et que l’on détermine qu’il existe une différence significative entre l’apport nutritif d’une grenouille et celle d’un mulot, cela ne veut pas nécessairement dire que cette différence soit importante pour le hibou. La différence pourrait être minuscule, de l’ordre de 10 calories (la taille de notre effet), mais tout de même être statistiquement significative puisque l’on aurait échantillonné des milliers de proies et que leur apport est extrêmement constant.

Rappelez-vous, comme nous avons discuté au Chapitre 10, que la puissance statistique (que l’on pourrait redéfinir ici comme la probabilité de trouver un effet significatif) dépend à la fois de la taille de l’échantillon, de la variabilité et de l’ampleur de l’effet que l’on recherche. Hors, pour le hibou, une seule de ces choses compte vraiment : la taille de l’effet, i.e. combien de calories cette proie m’apporte-t-elle de plus par rapport à une autre.

Dans les prochains chapitres, nous discuterons surtout de méthodes permettant de savoir si un constat est statistiquement significatif ou non. Beaucoup de gens y accordent encore beaucoup d’importance, mais sachez qu’il s’agit d’une approche qui tend à changer depuis quelques années. De plus en plus de scientifiques tendent plutôt vers une approche centrée vers l’estimation des tailles d’effet et d’une mesure de confiance associée. Vous verrez d’ailleurs plusieurs de ces approches dans la section de ce livre sur les modèles linéaires (e.g. du Chapitre 27 au Chapitre 31).

Dans cette partie sur les tests statistiques, je vous demanderai simplement que chaque fois que vous arriverez à un résultat, de ne pas vous arrêter à savoir si votre résultat et significatif ou non, mais d’aller plus loin et de (1) rapporter la taille de l’effet, mais aussi de (2) l’interpréter au mieux de votre connaissance sur le sujet. Cela fera déjà de vous d’excellents scientifiques, avec l’esprit allumé nécessaire pour passer aux méthodes plus avancées dans l’avenir.

12.3 Concept d’hypothèse statistique

Au début du Chapitre 10, nous avons discuté de comment développer de bonnes questions écologiques et de comment y associer des hypothèses de travail. Pour effectuer des tests statistiques, vous aurez besoin d’effectuer une étape supplémentaire, soit de construire des hypothèses statistiques, qui seront essentiellement des versions falsifiables statistiquement de nos hypothèses de travail. On pourra affirmer, à l’aide d’un chiffre, si elles sont fausses ou non.

Chacune de vos hypothèses de travail devra être transformée en une paire d’hypothèses statistiques que l’on nomme hypothèse nulle et hypothèse alternative. L’hypothèse nulle, souvent nommée H₀, décrit la situation en l’absence de l’effet, du changement et ou de la différence recherchés. L’hypothèse alternative, souvent nommée H₁, décrit la différence, le lien ou le changement que l’on recherche.

Si l’on reprend notre hypothèse de travail où l’on avançait que la présence du tangara écarlate devait être reliée à la présence de forêt mature, elle pourrait être traduite en ces deux hypothèses statistiques :

\[ \begin{aligned} H_0 : \mu_{\text{forêt mature}} = \mu_{\text{forêt jeune}}\\ H_1 : \mu_{\text{forêt mature}} > \mu_{\text{forêt jeune}} \end{aligned} \]

Autrement dit, pour H₀, nous disons que le nombre moyen de tangara sera le même en forêt mature que dans les forêts plus jeunes. L’hypothèse alternative, H₁, est que le nombre de tangara moyen par parcelle sera plus grand dans la forêt mature que dans la jeune forêt. Notez que les hypothèses font référence à la population, et l’on utilise donc le symbole μ pour définir la moyenne.

L’hypothèse H₀ doit être clairement falsifiable. On doit pouvoir montrer qu’elle est fausse. C’est le fondement de toute la démarche des tests d’hypothèses.

12.4 La prise de décision statistique

Une fois ces hypothèses mises en place, il reste maintenant à effectuer le test statistique comme tel. Le processus de prise de décision est relativement simple, mais le pourquoi de la chose mérite une petite réflexion.

Comme nous en avons discuté plusieurs fois depuis le début du cours, lorsque l’on effectue une expérience (i.e. que l’on pige un échantillon dans une population), il existe une variabilité associée à cette procédure. Tous nos échantillons ne seront pas parfaitement identiques. Et donc, dans les faits, H₀ ne sera jamais vraie au sens absolu du terme. Nos deux moyennes ne seront jamais parfaitement égales. Il n’y aura jamais une absence totale de liens entre deux variables. Il s’agit d’un constat clé à comprendre pour la suite.

P. ex. en l’absence de différence pour le tangara entre la forêt mature et la jeune forêt, il y aura toujours une différence entre nos échantillons matures et jeunes. Cette différence sera la plupart du temps petite, mais il pourrait arriver parfois que le hasard fasse que la moyenne entre nos échantillons soit très différente. De la même façon qu’il pourrait arriver, une fois de temps en temps, qu’en lançant 5 pièces de monnaie en l’air, elles retombent toutes du même côté.

Des mathématiciens ont donc préparé pour chacun des tests statistiques un petit calcul pour représenter le phénomène que l’on désire mesurer (différence de moyenne, lien entre deux variables, différence de proportions, etc.), que l’on nomme la statistique de test. Par la suite, il ont créé des lois de probabilités qui décrivent les fréquences attendues de ces statistiques de test, si l’hypothèse H₀ est vraie. La statistique de test n’a pas d’interprétation directe, elle est une étape intermédiaire au calcul du test statistique.

Sachant tout ceci, la prise de décision d’un test statistique est plutôt simple : on calcule la statistique de test à partir de nos échantillons, et on demande à R quelle est la probabilité d’avoir trouvé un tel résultat si H₀ est vraie. C’est ce que l’on appelle la fameuse valeur de p.

Si nous avons affaire à quelque chose de vraiment rare (i.e. peu probable si H₀ est vraie, donc une valeur de p faible), on dit que notre test est statistiquement significatif. C’est à dire qu’il serait peu probable d’avoir trouvé quelque chose d’aussi clair comme différence/lien/association si H₀ était vraie.

Qu’est-ce qui est assez rare pour être considéré comme statistiquement significatif? Toute probabilité qui est plus rare (i.e. petite) que le seuil de signification (α) pré-établit, qui est classiquement placé à 5 %.

Une fois que l’on a déterminé si notre résultat était statistiquement significatif ou non, on peut enfin se prononcer à savoir si l’on peut ou non rejeter l’hypothèse H₀. Certains scientifiques font un lien direct entre rejeter l’hypothèse H₀ et accepter l’hypothèse H₁, mais il faut demeurer prudent. Rejeter H₀ renforce notre croyance dans H₁, mais ce n’est pas une preuve à proprement parler, particulièrement si notre H₁ était un peu tirée par les cheveux.

12.5 Procédure recommandée

Donc, si l’on met tous ces morceaux ensemble, voici comment appliquer un test statistique :

Définir l’hypothèse nulle (H₀) et l’hypothèse alternative (H₁)
Explorer visuellement les données pour vérifier…
1. Le respect des assomptions du test
2. Que l’on peut voir, à l’oeil, l’effet recherché
Calculer la statistique de test
Obtenir la valeur de p de cette statistique de test dans la distribution appropriée
Décider de rejeter ou non l’hypothèse nulle
Citer la taille de l’effet et son intervalle de confiance

Lorsque vous effectuerez vos premiers tests statistiques, vous aurez probablement l’impression qu’il s’agit d’une tâche complexe, confuse, etc. C’est tout à fait normal, il y a beaucoup de matériel à digérer. Par contre, si je fais bien mon travail, au fil des semaines, cette tâche devrait devenir de plus en plus claire dans vos têtes, jusqu’à en devenir monotone et prévisible. Si vous en arrivez à ce point, j’aurai atteint mon objectif d’enseignement!

Remarquez que j’ai nommé à l’étape 2.a la vérification des assomptions. Dans d’autres cours ou avec d’autres profs, vous lirez peut-être un intitulé conditions d’application. J’essaie le plus possible d’éviter ce terme, car il laisse à penser que si une condition n’est pas remplie (par exemple la normalité), on ne peut strictement pas appliquer le test. Alors que dans les faits, les tests présentent pour la plupart une certaine robustesse à leur non-respect. Le terme assomption, quant à lui, fait référence au fait que, quand ils ont inventé le test, les mathématiciens prenaient pour acquis certaines choses à propos des données qu’on allait entrer. Si on entre autre chose, pour certains tests c’est OK jusqu’à un certain point, pour d’autres non.

12.6 Exercice : Les hypothèses

Afin de vous assurer que vous démêlez bien les différentes questions et hypothèses associées aux tests statistiques, placez au bon endroit ces quatre termes statistiques

Question,
Hypothèse de travail,
Hypothèse nulle (H₀),
Hypothèse alternative(H₁).

dans les deux mises en situation suivantes :

Effet des néonicotinoïdes sur les abeilles :

Il n’y a pas de différence entre le taux de décès moyen des abeilles exposées aux néonicotinoïdes et ceux qui n’y sont pas exposées.
Les néonicotinoïdes influencent négativement le taux de survie des abeilles.
Quelle est l’influence des néonicotinoïdes sur les populations d’abeilles?
Il existe une différence entre le taux de décès moyen des abeilles exposées aux néonicotinoïdes et ceux qui n’y sont pas exposées.

Fonctionnement du syndrome du museau blanc :

Il n’existe pas de différence entre le nombre de périodes d’éveil moyen des chauve-souris affectées par le syndrome du museau blanc et celles qui ne le sont pas.
Il existe une différence entre le nombre de périodes d’éveil moyen des chauve-souris affectées par le syndrome du museau blanc et celles qui ne le sont pas.
Comment le syndrome du museau blanc affecte-t-il la santé des chauve-souris?
Le syndrome du museau blanc augmente le nombre de périodes d’éveil pendant l’hibernation

12.7 Le test de T à un échantillon

Pour terminer cette initiation aux tests statistiques nous verrons ensemble un premier test, qui est à mon avis le plus simple et le plus facile à comprendre, c’est pourquoi je l’enseigne en premier. Il s’agit du test de T à un échantillon. Ce test permet de déterminer si la moyenne d’un échantillon est significativement différente d’une valeur cible.

Voyons un exemple de mise en situation où l’on peut utiliser le test de T à un échantillon. Vous employez normalement un engrais qui devrait permettre à vos plantes de pousser de 5 cm en une semaine. Vous trouvez un vieux pot de cet engrais, dont vous n’êtes plus certain de l’efficacité. Vous pourriez monter une petite expérience où vous faites pousser 25 plantes à l’aide de l’engrais. Vous pourriez ensuite utiliser le test pour savoir si elles ont effectivement grandit de 5 cm (en moyenne) durant la période ou si elles ont moins grandit (i.e. que votre engrais est périmé).

Étape 1 : Définir les hypothèses

Lorsque l’on applique le test de T à un échantillon, notre hypothèse H0 sera que la moyenne de la population est égale à la valeur de référence, p. ex. pour notre mise en situation : \[ \begin{aligned} H_0 : \mu = 5\ cm \\ H_1 : \mu \neq 5\ cm \end{aligned} \]

Étape 2 : Explorer visuellement les données

Le test de T à un échantillon assume essentiellement deux choses : que notre échantillon provient d’une distribution normale et que chacune de nos observations sont indépendantes les unes des autres. La façon la plus simple et intuitive de vérifier l’assomption de normalité est d’afficher l’histogramme de notre variable. On peut aussi ajouter à cet histogramme un trait vertical représentant la valeur de référence, afin de voir si à l’oeil nos données s’éloignent de la valeur de référence ou non, comme ceci :

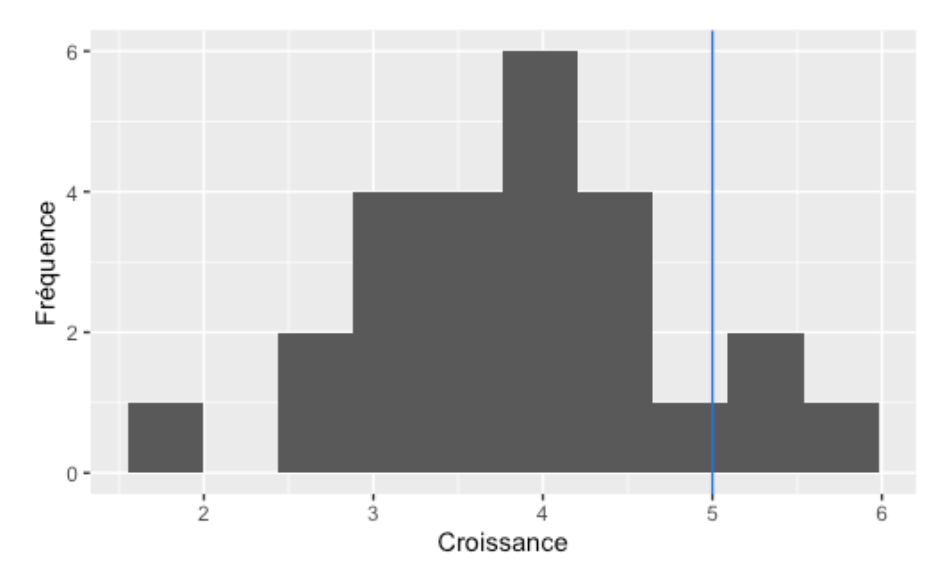
On peut constater principalement deux choses dans ce graphique. D’abord, la forme de nos données correspondent grossièrement à une loi normale. Il faut toujours garder en tête qu’avec de faibles tailles d’échantillon (comme ici avec 25), la forme de la courbe ne sera jamais parfaitement normale. Il faut entraîner notre œil à savoir ce qui est tolérable ou non. D’autant plus que le test de T lui même est robuste au non-respect de cette assomption. Il fournira des résultats fiables même si nos données s’éloignent de la normalité. Malheureusement, il n’existe pas de “seuil de non-normalité” à partir duquel on peut être certain que l’on est OK. Il faut utiliser notre jugement.

La deuxième chose que l’on constate dans ce graphique est que nos données semblent en général sous la barre des 5 cm de croissance. En regardant ce graphique, il faudra s’attendre à trouver un test significatif.

Étape 3 : Calculer la statistique de test

Pour le test de T à un échantillon, les mathématiciens ont défini la statistique de test comme ceci : \[t = \frac{\bar{x}-\mu_0}{s/\sqrt{n}}\] Autrement dit, notre statistique de test (t) est égale à la moyenne de l’échantillon, à laquelle on soustrait notre valeur de référence (ici 5 cm). On divise ensuite cela par l’erreur-type (i.e. notre incertitude par rapport à cette moyenne, voir Chapitre 11).

Comme je vous ai parlé dans d’autres chapitres, il n’est pas très productif d’apprendre par cœur la formule pour la statistique de t. Vous devez par contre comprendre que plus l’échantillon s’éloigne de la valeur de référence, plus t sera grand (en valeur absolue) et plus nos données sont variables, plus t sera petit (en valeur absolue).

Pour notre exemple, la moyenne de notre échantillon est de 3,89 cm et l’écart-type est de 0,91 cm. La statistique de test est donc de -6,1. Le fait que la valeur de t soit négative ou positive n’a pas d’importance dans la procédure de test, l’important est comment la valeur de t s’éloigne de zéro.

Étape 4 : Obtenir la valeur de p.

Après avoir calculé la statistique de test, il faut maintenant déterminer si trouver une telle valeur de t est rare ou non. Les mathématiciens ont déterminé que si on calculait la statistique de t pour une série d’échantillons ayant la même moyenne, la distribution résultante formerait ce qu’ils ont nommé la distribution de T de Student.

Cette distribution est très semblable à la distribution normale, mais sa forme se modifie selon la taille de l’échantillon. Pour y arriver, la distribution de T nécessite deux paramètres, soit la moyenne et les degrés de liberté de notre calcul.

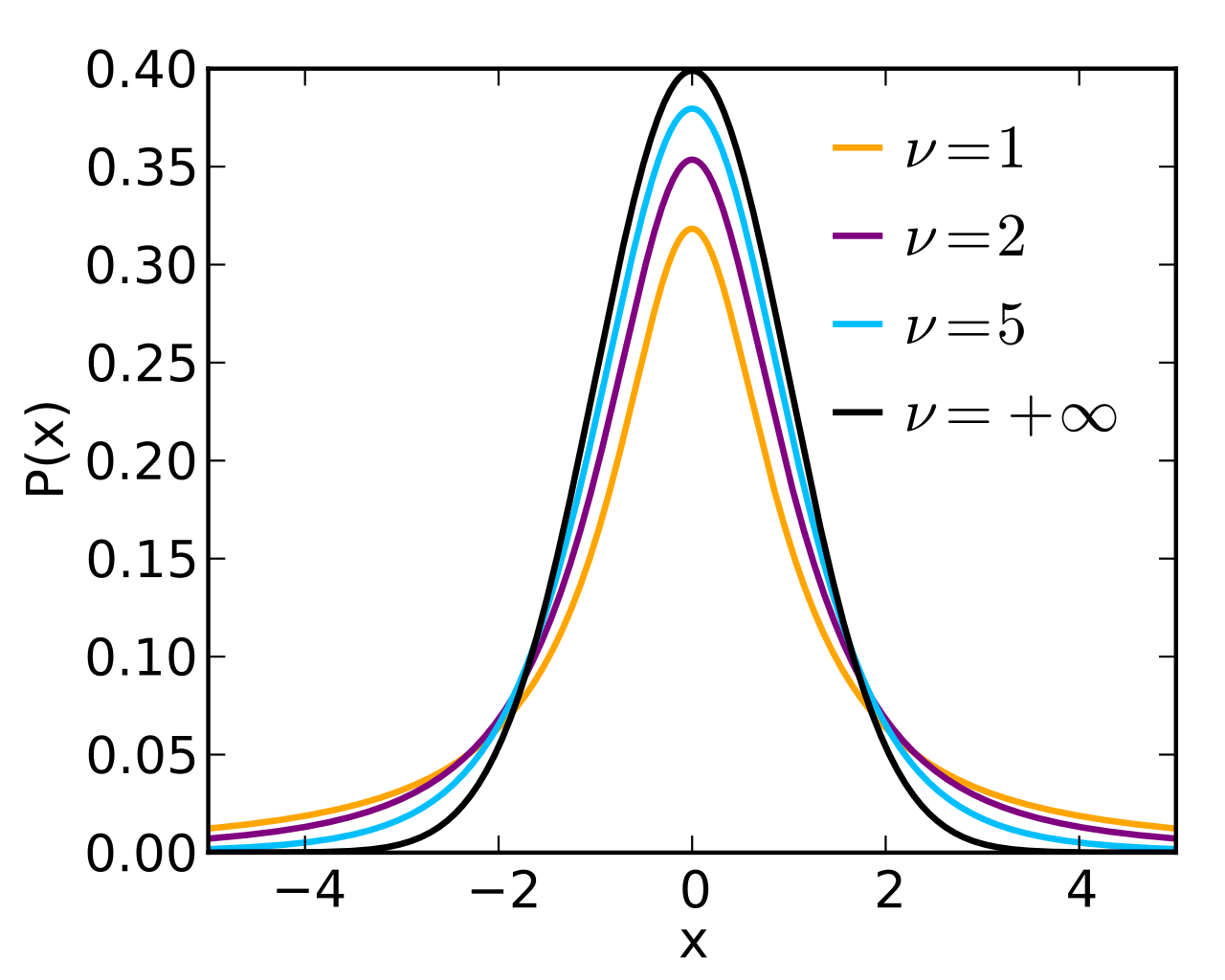
La distribution de T de student, pour 1, 2, 5 et infini degrés de liberté (ν). Skbkekas, CC BY 3.0, via Wikimedia Commons

Pour le test de t à un échantillon, les degrés de liberté sont définis comme ceci : \[d.d.l. = n - 1\]

Pour une valeur de t de -6,1 et 24 degrés de liberté, la chance d’obtenir quelque chose d’aussi différent de la valeur de référence ou encore plus différent, si H₀ est vraie, est de 0,0000026 (notre valeur de p).

Remarquez que je vous fournis la valeur de p sans vous dire exactement comment elle a été calculée. Comme la formule pour l’obtenir est super complexe ¹ et que vous n’aurez jamais à la calculer manuellement, je vous épargne cette étape. J’espère que vous ne m’en voudrez pas trop! Si vous voulez vraiment récupérer cette valeur par vous-même, vous pouvez lancer la fonction R pt, comme ceci avec une valeur de t négative:

pt(-6.1,24)*2

[1] 2.665881e-06

Et comme ceci pour une valeur positive :

(1-pt(6.1,24))*2

[1] 2.665881e-06

R vous retournera alors la bonne valeur de p pour le t et les degrés de liberté appropriés. Remarquez qu’il faut multiplier la valeur de p par deux, car nous voulons effectuer un test bilatéral, donc en séparant la probabilité de chaque côté de la distribution.

Étape 5 : Rejeter ou non l’hypothèse nulle

À ce point, nous pouvons maintenant prendre notre décision statistique. Ici, puisque notre événement est plus rare que le seuil de signification (p < 0,05), on peut affirmer que l’on rejette l’hypothèse nulle. Notre moyenne est significativement différente de la valeur de référence de 5 cm.

Étape 6 : Citer la taille de l’effet et son intervalle de confiance.

Dans le cas du test de T à un échantillon, le chiffre qui nous intéresse est la moyenne de notre échantillon. Dans notre cas, 3,89 cm de croissance. On peut donc juger de l’importance de ce phénomène en constatant que notre échantillon était plus d’un cm plus court que la valeur de référence. Pour nous aider à juger de la confiance à avoir dans ce résultat, il est recommandé de l’accompagner de son intervalle de confiance.

L’intervalle de confiance à 95 % d’une moyenne se calcule comme ceci : \[\bar{x} = t_{0,05}\frac{s}{\sqrt{n}}\]

Où t_0,05 la valeur de T associée à la probabilité de 5 %. Il faut faire attention cependant car puisque notre intervalle de confiance est bilatérale, dans les faits, il faut chercher la valeur associée à la probabilité de 0,025.

Pour notre exemple, l’intervalle de confiance autour de notre moyenne est donc de 3,89 ± 0,37, soit entre 3,52 et 4,27 cm. Vous remarquerez que, chaque fois que vous obtiendrez un test significatif au seuil de 5 %, l’intervalle de confiance à 95 % exclura toujours la valeur de référence.

Dans un rapport, vous pourriez écrire ce résultat comme ceci : « La croissance moyenne des plantes était de 3,89 cm ± 0,37 (I.C. 95 %), ce qui était significativement différent des 5 cm attendus avec l’engrais (t₂₄ = 6,1, p = 0,00000026). » Remarquez que l’on nomme toujours verbalement le résultat, et on ajoute entre parenthèses l’information statistique pour le supporter.

Vous verrez souvent les valeurs de p significatives inscrites uniquement comme p < 0,05 ou p < 0,01, etc., mais ce format rend difficile la vérification de vos résultats ou leur réplication. À mon avis, il vaut mieux toujours rapporter les valeurs exactes.

12.8 Labo : Le test de T à un échantillon

Maintenant, voyons comment effectuer votre premier test statistique dans R. Vous serez rassuré de voir que tout le détail des étapes 3 et 4 de la démarche présentée ci-haut se résume à une seule ligne de code, qui fait tout pour vous!

Pour notre petit laboratoire, nous tenterons de répondre à la question : est-ce que les manchots Chinstrap de l’archipel Palmer se distinguent des autres populations de manchots Chinstrap, pour lesquels nous savons que le poids moyen est de 4250 g². Étant donné que l’archipel est situé à l’extrême sud de la distribution de l’espèce, notre hypothèse de travail sera que les manchots de l’archipel auront un poids différent du 4250 g de référence.

Étape 1 :

Nos hypothèses statistiques seront donc : H₀ : µ = 4250 g H₁ : µ ≠ 4250 g

Étape 2 :

Pour faciliter notre travail, nous allons nous préparer un petit tableau de données contenant uniquement les manchots Chinstrap pour lesquels nous connaissons le poids.

library(tidyverse)

── Attaching core tidyverse packages ──────────────────
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     
── Conflicts ───────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

library(palmerpenguins)

chinstrap <- penguins |> 
  filter(species == "Chinstrap") |> 
  drop_na(body_mass_g)

ggplot(data = chinstrap) +
  geom_histogram(mapping = aes(x = body_mass_g)) +
  geom_vline(xintercept = 4250, color = "royalblue")

`stat_bin()` using `bins = 30`. Pick better value with
`binwidth`.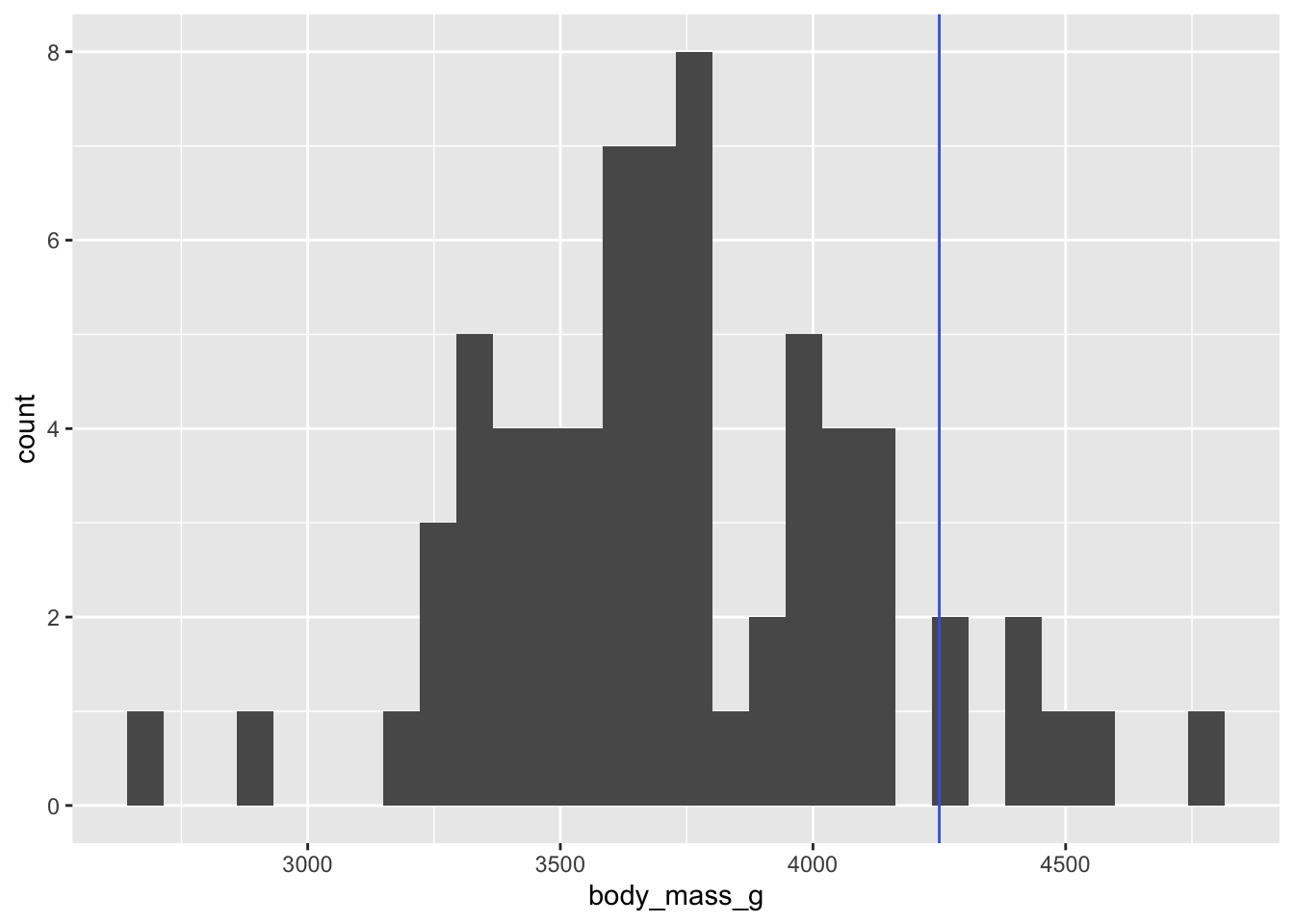

Donc, à première vue, l’assomption de normalité semble respectée pour cette variable. Pour ce que l’on en sait, nos observations sont indépendantes les unes des autres.

Enfin, à première vue, le poids des manchots Chinstrap de l’archipel Palmer semble situé près de 3750, ce qui est bien en dessous de la moyenne de l’espèce. Il faudra sans doute s’attendre à trouver un effet significatif.

Étapes 3 et 4 :

Les étapes 3 et 4 peuvent être résumées en une seule ligne de R, qui va à la fois calculer la statistique de test et déterminer la valeur de p associée, avec les bons degrés de liberté etc. :

t.test(chinstrap$body_mass_g, mu = 4250)

La fonction t.test, contrairement à celles des librairies ggplot2 et dplyr, n’est pas conçue pour travailler avec des tableaux de données. Elle s’attend plutôt à recevoir une simple série de nombres, que l’on nomme vecteur dans R. Pour extraire un vecteur d’un tableau de données, R nous offre l’opérateur $. Vous pouvez d’ailleurs voir le contenu du vecteur directement, comme ceci :

chinstrap$body_mass_g

 [1] 3500 3900 3650 3525 3725 3950 3250 3750 4150 3700
[11] 3800 3775 3700 4050 3575 4050 3300 3700 3450 4400
[21] 3600 3400 2900 3800 3300 4150 3400 3800 3700 4550
[31] 3200 4300 3350 4100 3600 3900 3850 4800 2700 4500
[41] 3950 3650 3550 3500 3675 4450 3400 4300 3250 3675
[51] 3325 3950 3600 4050 3350 3450 3250 4050 3800 3525
[61] 3950 3650 3650 4000 3400 3775 4100 3775

Le deuxième argument (mu) indique à R quelle valeur de référence nous voulons utiliser pour notre test de T à un échantillon. Si on omet cet argument, R assumera que la valeur de référence est zéro.

Après avoir lancé notre commande de test de T, R nous répond ceci :


    One Sample t-test

data:  chinstrap$body_mass_g
t = -11.091, df = 67, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 4250
95 percent confidence interval:
 3640.059 3826.117
sample estimates:
mean of x 
 3733.088

La première ligne nous indique que R a appliqué un test de T à un échantillon (One Sample t-test). La deuxième (data:) nous indique sur quelles données a été calculé le test. La ligne suivante nous montre la valeur de t calculée, les degrés de liberté (df, pour Degrees of Freedom) et la valeur de p (p-value) de notre test. La ligne suivante (alternate hypothesis…) nous informe de notre hypothèse alternative, soit que la moyenne est différente de 4250. Les dernières lignes nous fournissent l’intervalle de confiance à 95 % de notre moyenne, soit une moyenne de 3733 et un intervalle de confiance allant de 3640 à 3826.

Remarquez la façon dont R nous rapporte la valeur de p de notre test : < 2.2e-16.

Tout d’abord, plutôt que nous fournir la valeur en notation décimale, R nous la fournit en notation scientifique. 2.2e-16 est sa façon de dire 2.2 x 10^-16, soit 0.00000000000000022 (i.e. on a besoin de 16 zéros pour l’écrire).

Ensuite, bien que R soit capable de calculer très précisement les valeurs de p, la notre est tellement petite que R ne peut pas nous fournir le chiffre exact. Il peut seulement nous dire que c’est plus petit que 2.2 x 10^-16. Mais n’ayant crainte, dans la vraie vie, cela vous arrivera très rarement.

Étape 5 :

Comme notre valeur de p est plus rare que le seuil de signification de 0,05, nous rejetons l’hypothèse nulle H₀ qui stipulait que les manchots Chinstrap de Palmer auraient le même poids que le reste de l’espèce. Nous favorisons donc notre hypothèse H₁ qui avançait que leur poids moyen serait différent de 4250.

Étape 6 : Voici ce que nous pourrions écrire comme résultats pour présenter notre découverte : « Le poids moyen des manchots Chinstrap de l’archipel Palmer était de 3733 g ± 93 g (I.C. 95 %), ce qui était significativement différent des 4250 g attendus si leur poids correspondait à la moyenne de l’espèce (t₆₇ = -11,091, p < 2.2 x 10^-16). »

Remarquez que 3733 g ± 93 n’est qu’une façon alternative d’écrire l’intervalle 3640 à 3826. Une façon ou l’autre est acceptée comme façon de décrire l’intervalle.

12.9 Contenu optionnel : Appliquer un test statistique à l’ancienne.

La section qui suit est à titre informatif seulement. Elle pourrait même entraîner une certaine confusion. Libre à vous de la lire ou non.

À l’époque où les tests statistiques ont été développés, les scientifiques n’avaient pas accès aux ordinateurs ultra-rapides d’aujourd’hui. Calculer la valeur de p exacte comme nous l’avons fait ci-haut en quelques secondes pouvait prendre des heures de calcul manuel. C’est pourquoi les scientifiques ont longtemps utilisé une approche légèrement différente pour appliquer leurs tests, qui est encore parfois enseignée.

Les étapes 1, 2, 3 et 6 du processus étaient les mêmes, mais les étapes 4 et 5 étaient différentes. En fait, l’étape 4 du calcul de la valeur de p était carrément absente. Les scientifiques utilisaient plutôt une série de tables, remplies de chiffres, dans lesquels on pouvait trouver les valeurs de t correspondant à un seuil de signification et à un degré de liberté donné. Voici p. ex. un extrait d’une de ces tables pour la distribution de T de Student :

d.d.l / α	0,05	0,025	…
1	6,314	12,076	…
2	2,920	4,303	…
3	2,353	3,182	…
…	…	…	…

Extrait de la table des valeurs seuils pour la distribution de T de Student.

Les dernières pages des manuels de statistiques étaient remplies de ce genre de tables. Pour les utiliser, le scientifique décidait d’abord du seuil de signification de son expérience (habituellement 0,05) et déterminait les degrés de liberté. Il allait par la suite consulter la table pour savoir quelle valeur de t il devait dépasser (en valeur absolue) pour considérer son test comme significatif. La décision était donc prise en comparant les valeurs de t plutôt qu’en comparant une valeur de p à un seuil de signification.

Comptez-vous chanceux d’apprendre l’analyse statistique aujourd’hui, parce que lorsque j’ai suivi mon cours de biostatistiques il n’y a pas si longtemps (2010), c’était encore la façon de faire qui était enseignée, et une fois sur deux, on perdait des points en se trompant en consultant la table!

12.10 Tests unilatéraux ou bilatéraux

Vous avez probablement remarqué dans les exemples de tests de t ci-haut, que j’ai toujours parlé de regarder si notre échantillon était différent de la valeur seuil, plutôt que spécifiquement chercher si il était plus grand ou plus petit. Il existe une excellente raison derrière cette décision! Lorsque nous effectuons un test qui cherche une différence (quelle que soit la direction), le seuil de signification est réparti de façon égale, moitié-moitié de chaque côté de la distribution. Ces zones sont donc petites, et notre test est réputé être conservateur, c’est-à-dire peu à risque d’erreur de type I. Si nous choisissons de regarder uniquement si la moyenne de notre échantillon est plus petite (ou plus grande selon les cas) que notre valeur seuil, alors l’ensemble de la zone de signification se retrouve du même côté :

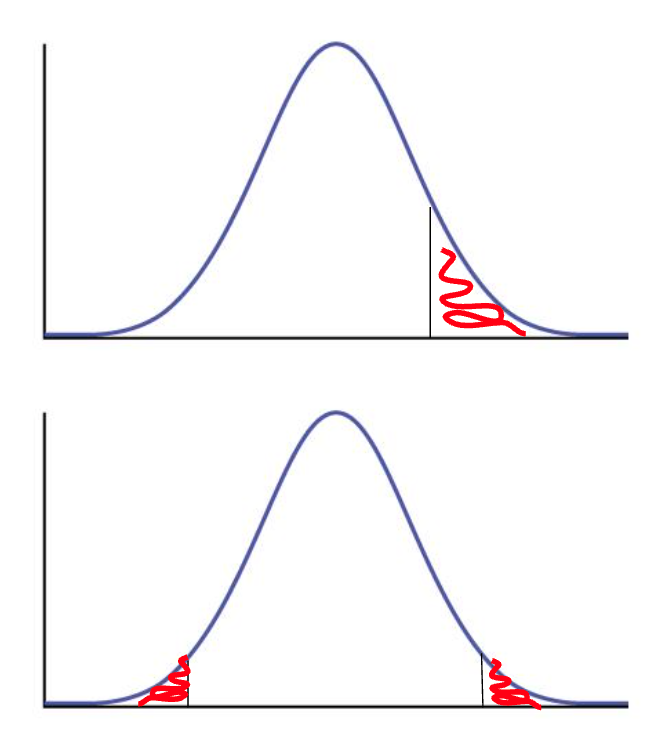
Illustration de la différence de la zone se signification entre un test unilatéral (en-haut) et un test bilatéral (en-bas).

Pour les cas où votre valeur de p est extrêmement faible ou très grande, faire un test unilatéral ou bilatéral ne fera aucune différence. Par contre, si votre résultat se trouve dans la zone qui passe du rouge au blanc entre les deux types de tests, vous pourriez être accusé d’avoir “gonflé” vos résultats si vous utilisez un test unilatéral.

Donc, à moins de raisons conceptuelles et théoriques extrêmement solides, utilisez toujours un test bilatéral. Il s’agit là d’une pratique à bien intégrer à vos habitudes d’analyse de données : en cas de doutes, optez toujours pour la solution la plus conservatrice, c’est-à-dire celle qui minimisera votre risque d’erreur de type I.

Si néanmoins vous désirez effectuer un test de t unilatéral, vous pouvez spécifier de quel côté va votre hypothèse H₁ à l’aide de l’argument nommé alternative :

t.test(chinstrap$body_mass_g, my = 4250, alternative = "less")


    One Sample t-test

data:  chinstrap$body_mass_g
t = 80.096, df = 67, p-value = 1
alternative hypothesis: true mean is less than 0
95 percent confidence interval:
     -Inf 3810.826
sample estimates:
mean of x 
 3733.088

Si vous vouliez tester spécifique pour plus grand que 4250, inscrivez “greater” plutôt que “less”

12.11 Contenu optionnel : Sur l’importance de la taille de l’effet

Pour terminer ce chapitre, je vais vous raconter une petite anecdote personnelle illustrant bien l’importance d’évaluer la taille de l’effet, même si un résultat est statistiquement significatif.

Lorsque ma conjointe était enceinte de notre deuxième enfant, elle est venue me voir un peu en panique un matin, après avoir lu un article qui disait que les femmes de petite taille avaient plus de risque d’accoucher prématurément³. L’article de vulgarisation sur lequel elle était tombée ne mentionnait qu’un seul chiffre, soit la taille de l’échantillon, mais aucune mention sur le risque comme tel, de combien de jours plus courte était la grossesse des femmes de plus petite taille, etc.

Mon esprit de scientifique m’a apporté sur Google Scholar où j’ai retracé l’article original⁴. Dans ce dernier, on insistait beaucoup sur le fait que les résultats étaient extrêmement significatifs, la valeur de p étant de 0,000000151. Par contre, ils insistaient très peu sur le fait que la taille de l’effet n’était que de 0,3 jours de grossesse de moins par tranche de 1 cm de grandeur de la mère. Un petit calcul rapide pour ma conjointe, qui est particulièrement petite (10 cm sous la moyenne des femmes au Canada), nous donne un gros 3 jours de moins de grossesse que la moyenne. Sachant que la grossesse est déjà un phénomène extrêmement variable, qui dure 95 % du temps entre 260 et 300 jours, cette différence de 3 jours était somme toute peu importante.

Si les auteurs de l’étude avaient mis de l’avant la taille de l’effet plutôt que le fait que leur résultat était hautement significatif, ils auraient évité beaucoup de stress inutile (et en fait, on n’aurait peut-être même pas discuté de leur étude dans les journaux grands-public).

Morale de l’histoire, mettez toujours, svp, l’emphase sur la taille de l’effet dans vos résultats!