ratons <- matrix(data = c(2,22,27,41), ncol = 2, byrow = TRUE)19 La comparaison de proportions
Dans ce chapitre, nous discuterons de l’analyse des variables catégoriques. Vous vous rappelez peut-être qu’au Chapitre 3, nous avons vu qu’une façon de travailler avec les variables catégoriques était de compter le nombre de fois que chacune des combinaisons de valeurs revenait, et d’illustrer ces informations dans un diagramme à bandes ou un tableau de contingence.
On pourrait par exemple se demander si l’efficacité de la vaccination contre la rage chez les ratons-laveurs est affectée par la saison. Pour notre expérience, nous avons bombardé une région de vaccins oraux contre la rage enrobés de nourriture. Nous avons ensuite capturé autant de ratons-laveurs que possible et analysé en laboratoire si ils étaient atteints ou non du virus. La base de données qui en résulterait, selon les principes des données propres, pourrait ressembler à ceci :
| Individu | Saison | Rage |
|---|---|---|
| A | Printemps | Positif |
| B | Printemps | Négatif |
| C | Printemps | Positif |
| D | Automne | Positif |
| E | Automne | Négatif |
| … | … | … |
On constate donc que les deux variables qui nous intéressent sont des variables catégoriques (Saison et Rage). Il faut donc transformer nos données en tableau de contingence pour les analyser, soit comme ceci :
| Positif | Négatif | |
|---|---|---|
| Automne | 2 | 22 |
| Hiver | 27 | 41 |
Vous voyez qu’une fois transformées en tableau de contingence, les colonnes et les lignes du nouveau tableau représentent les valeurs de nos variables catégoriques originales.
Remarquez bien que dans un tableau de contingence, chaque individu ne doit apparaître qu’une seule fois et aussi que le contenu de chacune des cellules est une fréquence (i.e. un décompte).
Il ne faut jamais, même si c’est tentant, y inscrire des proportions ou des pourcentages. Nous testerons pour des différences de proportions, mais les données doivent être des fréquences.
Pour avoir une meilleure idée de ce qui se passe dans le tableau de contingence, on calcule souvent des totaux marginaux, c’est-à-dire que l’on calcule dans la marge le total pour chacune des lignes et colonnes, comme ceci :
| Positif | Négatif | Total | |
|---|---|---|---|
| Automne | 2 | 22 | 24 |
| Hiver | 27 | 41 | 68 |
| Total | 29 | 63 | 92 |
On constate donc deux choses dans ces totaux marginaux. En général, le nombre de ratons-laveurs capturés à l’automne est plus faible que celui capturés à l’hiver (24 vs. 68). En général, il y a moins de cas positifs que de cas négatifs à la rage (29 vs. 63). Évidemment, comme la nature est variable, le ratio positif/négatif n’est pas exactement le même entre les deux saisons. De la même façon, le ratio automne/hiver n’est pas exactement le même chez les cas négatifs que chez les cas positifs. Ce qui nous intéressera de savoir ici est de trouver si la proportion de cas positifs varie de façon systématique entre les saisons.
Remarquez que même si cela nous intéresse moins dans ce cas-ci, tester cette association entre les deux variables veut aussi dire que l’on teste si la proportion automne/hiver est différente selon que les ratons-laveurs sont positifs ou négatifs à la rage. L’association va toujours dans les deux sens.
19.1 Le test de khi-carré pour un tableau 2x2
Le test classique pour tester cette question d’association entre deux variables catégoriques est le test de khi-carré. Khi étant la lettre grecque, vous le verrez aussi appelé chi-carré (en anglais khi s’écrit chi), χ² ou même khi-deux. Il s’agit toujours du même test!
Nous utiliserons pour illustrer le test de khi-carré l’exemple avancé en introduction, soit de savoir si l’efficacité du vaccin contre la rage pour les ratons-laveurs varie entre les saisons.
Étape 1 : Définir les hypothèses
H0 : Il n’y a pas d’association entre la saison et le succès du vaccin
H1 : Il y a une association entre la saison et le succès du vaccin
Remarquez que pour ce test, il n’existe pas de façon mathématique officielle d’écrire les hypothèses (ou du moins, pas dans les 3 manuels de stats que j’ai consultés). On aurait par contre pu dire pour H0 que les variables étaient indépendantes et pour H1 qu’elles étaient dépendantes l’une de l’autre.
Étape 2 : Explorer les données
Comme suggéré précédemment, le test de khi-carré assume d’abord deux choses à propos de notre tableau de contingence. Ce dernier doit absolument contenir des fréquences, et chaque individu ne doit être représenté qu’une seule fois dans le tableau. Notez qu’ici le terme individu est utilisé de façon très générale, si votre étude porte sur les écosystèmes, il faudrait bien entendu que chaque écosystème ne soit représenté qu’une seule fois, etc. Il faut être très attentif à la structure du tableau, en particulier si ce n’est pas nous qui l’avons construit. Pour notre exemple sur la rage, il aurait pu arriver que quelqu’un vous envoie les données sous ce format :
| Cas positifs | Individus testés | |
|---|---|---|
| Automne | 2 | 24 |
| Hiver | 27 | 68 |
Ce dernier tableau n’est PAS approprié pour le test de khi-carré, même si à première vue, il est très semblable au précédent. Les individus positifs sont présents à la fois dans les deux colonnes!
Avant de décrire la troisième et dernière assomption du test de khi-carré, il importe de définir le concept de fréquence attendue. Rappelez-vous d’abord que l’hypothèse nulle de notre test est que les deux variables ne sont pas associées entre elles. Les fréquences attendues sont donc celles que l’on retrouverait dans le tableau de contingence si jamais les deux variables étaient totalement indépendantes les unes des autres.
Comment trouver ces fréquences attendues? Pour chacune des cellules du tableau de contingence, on multiplie les totaux marginaux de chaque cellule puis on les divise par le grand total. Par exemple, la fréquence attendue des cas positifs en automne serait de (24 x 29) / 92 = 7,57.
Le tableau des fréquences attendues ressemblerait donc à ceci :
| Positifs | Négatifs | |
|---|---|---|
| Automne | 7,56 | 16,43 |
| Hiver | 21,43 | 46,57 |
Ces données correspondent aux fréquences (théoriques) que l’on aurait dû observer en absence de bruit si jamais l’hypothèse nulle de notre test était vraie.
On peut maintenant énoncer la troisième assomption du test de khi-carré, soit que 80 % des cellules du tableau des valeurs attendues doivent contenir des valeurs d’au moins 5, et qu’aucune ne doit contenir une valeur < 1. Lorsque, comme ici, notre tableau de contingence est de 2x2, chacune des cellules doit être au moins de 5.
Étape 3 : Calculer la statistique de test
Une fois toutes ces choses énoncées, le calcul de la statistique du test de khi-carré est relativement intuitif :
\[ \chi^2 = \sum_{i=1}^n\frac {(|O_i-E_i|-0.5)^2} {E_i} \]
Où Oi est la valeur observée dans chaque cellule et Ei est la valeur attendue. Autrement dit, plus les fréquences observées sont différentes des fréquences attendues, plus la valeur du khi-carré sera élevée. La partie -0,5 se nomme la correction de Yates. Elle sert à éliminer le biais possible lié à l’analyse de tableaux 2x2. Pour des tableaux plus grands comme dans la section suivante, cette correction n’est pas nécessaire.
Si l’on effectue ce calcul pour notre exemple, nous arrivons à une valeur de khi-carré de 6,70.
Étape 4 : Obtenir la valeur de p
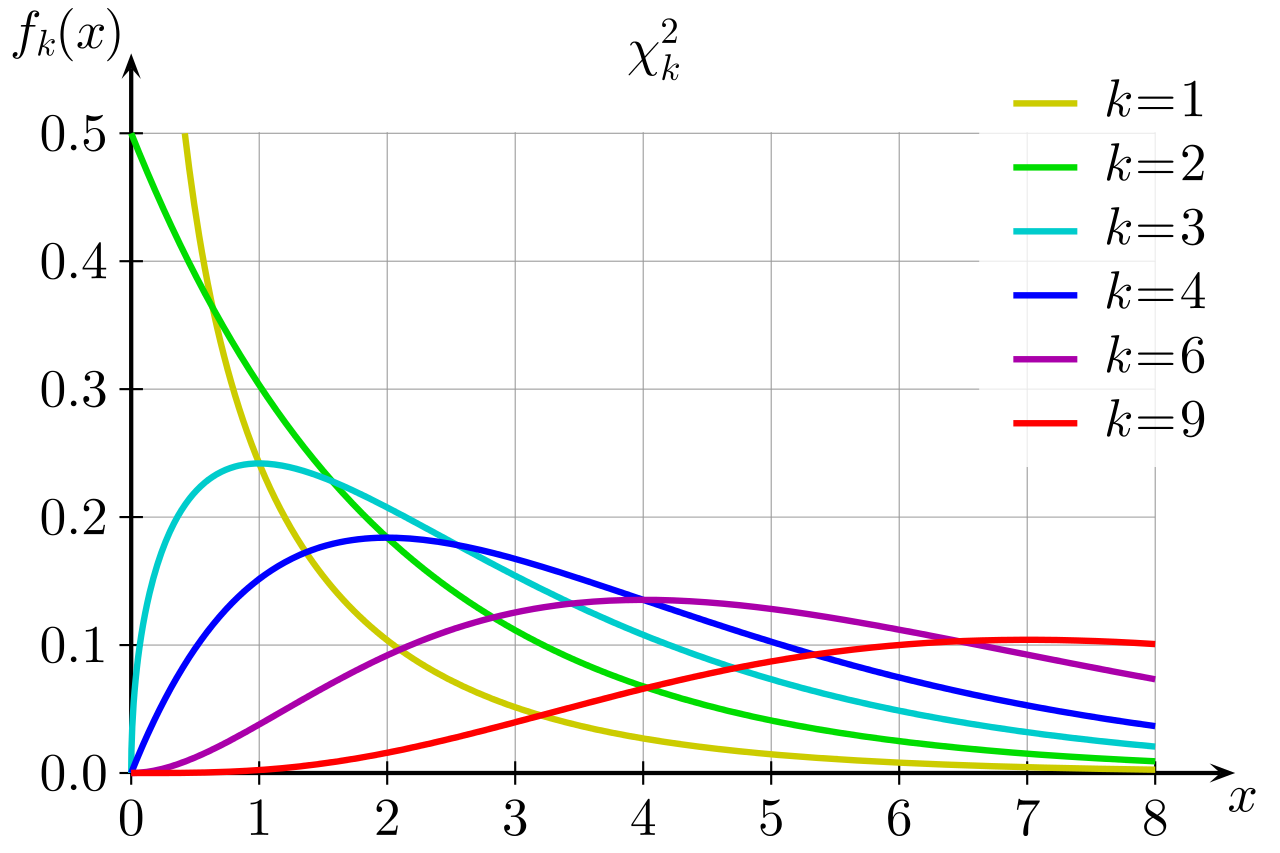
Contrairement aux tests des chapitres précédents, mais de façon un peu prévisible si vous avez saisi la nomenclature des tests statistiques, la distribution de notre statistique de test si l’hypothèse nulle est vraie suivra une distribution de… khi-carré! La distribution de khi-carré est particulièrement asymétrique, mais devient de plus en plus symétrique à mesure que les degrés de liberté augmentent (nommés k dans la figure) :
Les degrés de liberté du test de khi-carré sont définis comme étant (nombre de lignes - 1) x (nombre de colonnes - 1). Pour notre test de 2x2, nous avons donc un seul degré de liberté.
La probabilité associée à une valeur de khi-carré de 6,70 avec un seul degré de liberté est de 0,009639.
Étape 5 : Rejeter ou non l’hypothèse nulle.
Même si nous avons été chercher notre valeur de p dans une nouvelle distribution, c’est quand même la même poutine que les autres tests pour la suite.
La valeur de p est plus petite que le seuil de 0,05. Il serait donc très rare d’avoir une valeur de khi-carré aussi élevée si jamais nos deux variables n’étaient pas associées. On peut donc dire que l’on rejette l’hypothèse nulle qui stipulait que nos variables n’étaient pas associées.
On pourrait écrire notre résultat comme ceci : «Le succès du vaccin contre la rage chez les ratons-laveurs était significativement relié à la saison où se tenait l’opération de vaccination (χ21 = 6,70, p = 0,0096)».
19.2 Le test de khi-carré pour un tableau autre que 2x2
Le test de khi-carré s’effectue toujours pour évaluer l’indépendance entre deux variables catégoriques. Il peut cependant arriver qu’une (ou les deux) variables possèdent plus de deux valeurs possibles. On aurait pu, par exemple, analyser plutôt les données suivantes :
| Positifs | Négatifs | Non-concluant | |
|---|---|---|---|
| Printemps | 2 | 22 | 1 |
| Été | 27 | 41 | 12 |
| Automne | 20 | 21 | 3 |
| Hiver | 5 | 15 | 1 |
L’ensemble de la procédure demeure exactement le même, sauf que l’on enlève la correction de Yates au moment de faire le calcul du khi-carré, comme ceci :
\[ \chi^2 = \sum_{i=1}^n\frac {(O_i-E_i)^2} {E_i} \]
Remarquez qu’au final, le test ne peut pas nous dire dans quelle(s) cellule(s) survient la différence. On ne peut pas savoir si la différence provient des tests négatifs en automne, etc. On ne peut répondre qu’à la question : est-ce que les deux variables sont associées.
19.3 Labo : le test de khi-carré dans R
Jusqu’à présent, toutes les données que nous avons travaillées dans R se retrouvaient dans ce qu’on a appelé des tableaux de données (des objets data.frame ou tibble). Pour certaines fonctions, nous avions besoin d’accéder directement à une colonne à l’aide du $, mais d’une façon ou d’une autre, nos données étaient sous forme de tableaux.
Le test du khi-carré lui s’attend à recevoir un autre format, soit une matrice de données (matrix). Les matrices de données dans R sont aussi formées de données rectangulaires, mais elles ne peuvent contenir qu’un seul type de données à la fois. Elles doivent contenir soit des chiffres, soit du texte, mais il ne peut pas y avoir de mélange des deux dans une même matrice.
La saisie manuelle de matrice dans R s’effectue avec la fonction matrix. Il existe des dizaines de façons différentes d’utiliser cette fonction. Je vous en montrerai une, qui devrait convenir pour tout ce que nous aurons à faire dans ce livre (vous pouvez explorer les autres avec la commande ?matrix qui vous fournit l’aide de cette fonction). Par exemple pour entrer l’exemple ci-haut dans R, nous aurions pu faire comme ceci :
On passe donc à la fonction matrix 3 arguments. Le premier est la série de nombres à utiliser pour remplir la matrice, le deuxième est le nombre de colonnes (le nombre de lignes sera calculé automatiquement) et le troisième indique à R que l’on fournit nos données ligne par ligne. Si on regarde le contenu de notre matrice raton, on devrait voir ceci :
ratons [,1] [,2]
[1,] 2 22
[2,] 27 41Cette méthode fonctionne bien si nous avons déjà calculé notre tableau de contingence. Si ce n’est pas le cas, nous verrons dans l’exemple plus bas comment calculer directement le tableau de contingence à partir de nos données brutes.
Sachant que le ratio mâle-femelle est extrêmement variable chez le manchot royal1, on peut se demander si ce dernier varie aussi d’une année à l’autre chez les manchots de l’archipel Palmer.
Étape 1 :
H0 : Il n’y a pas d’association entre l’année et le sexe
H1 : Il y a une association entre l’année et le sexe
Étape 2 :
À cette étape, il faut d’abord préparer notre matrice de données, puisque le tableau de données n’est pas un tableau de contingence. Plutôt que de préparer la matrice manuellement, on peut utiliser la fonction table pour la construire. Cette dernière s’attend à recevoir les deux colonnes catégoriques qui formeront notre tableau de contingence. Cependant, on doit d’abord nettoyer nos données, puisque plusieurs individus n’ont pu être sexés lors de l’expérience.
library(palmerpenguins)
Attaching package: 'palmerpenguins'The following objects are masked from 'package:datasets':
penguins, penguins_rawlibrary(tidyverse)── Attaching core tidyverse packages ──────────────────
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.2 ✔ tibble 3.3.0
✔ lubridate 1.9.4 ✔ tidyr 1.3.1
✔ purrr 1.0.4 ── Conflicts ───────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorspour_chi_carre <- penguins |>
drop_na(sex)
ma_matrice <- table(pour_chi_carre$sex, pour_chi_carre$year)
ma_matrice
2007 2008 2009
female 51 56 58
male 52 57 59À première vue, la proportion mâle-femelle semble être très constante entre les années, très proche du 1:1, avec chaque fois légèrement plus de mâles.
Comme nous savons que chaque individu n’est représenté qu’une seule fois dans notre tableau de données, on sait que les deux premières assomptions du test sont respectées. La troisième assomption, pour les valeurs attendues >5 sera validée une fois le calcul complété, puisque R nous fournira aussi les valeurs attendues dans notre objet de résultats.
Étapes 3 et 4 :
Le test de khi-carré dans R s’effectue avec la fonction chisq.test (CHI-SQuared test). On lui passe notre matrice de données et c’est tout! R s’occupe tout seul de calculer les valeurs attendues, la statistique de test et décider d’appliquer ou non la correction de Yates.
resultat <- chisq.test(ma_matrice)On conserve le résultat du calcul dans un objet, car on a plusieurs opérations à faire avec.
Tout d’abord, il faut aller consulter le tableau des valeurs attendues pour s’assurer que l’on respecte les conditions d’application du test.
resultat$expected
2007 2008 2009
female 51.03604 55.99099 57.97297
male 51.96396 57.00901 59.02703Ici, toutes les valeurs sont bien au-delà de 5, donc aucun stress.
On peut maintenant regarder les résultats du test comme tel :
resultat
Pearson's Chi-squared test
data: ma_matrice
X-squared = 7.8283e-05, df = 2, p-value = 1Cette sortie contient très peu d’informations comparé à la régression linéaire. Nous avons la valeur de khi-carré calculée (7,8 x 10-5), les degrés de liberté (2) et la valeur de p associée (1).
Étape 5 :
Comme cet événement est relativement commun lorsque notre hypothèse nulle est vraie (p > 0,05), on considère qu’un tel résultat n’est pas significatif. On ne peut PAS rejeter l’hypothèse nulle qu’il n’y a pas d’association entre nos variables.
Étape 6 :
Il n’y a pas de taille d’effet comme tel à rapporter pour le test de khi-carré. On peut cependant écrire notre résultat comme ceci : « Il n’y a pas d’association significative entre l’année et le sexe (χ2=7,8 x 10-5, p = 1) »
19.4 Labo : le test exact de Fisher
Le test de khi-carré n’est pas le seul test conçu pour analyser des tableaux de contingence. Les mathématiciens en ont aussi conçu d’autres, entre autres, le test exact de Fisher.
Ce dernier est beaucoup plus complexe à calculer. Le principe de base est néanmoins plutôt simple et je vous l’expliquerai ici. Le test de Fisher explore tous les tableaux de contingence qui auraient pu exister en conservant les totaux marginaux de notre tableau original. Par exemple, pour un tableau de contingence de 2x2 avec les observations suivantes :
| 3 | 1 |
| 1 | 3 |
On calcule les totaux marginaux :
| 3 | 1 | 4 |
| 1 | 3 | 4 |
| 4 | 4 | 8 |
Et ensuite, R cherchera tous les tableaux permettant de respecter ces totaux, p. ex.
| 2 | 2 |
| 2 | 2 |
| 0 | 4 |
| 4 | 0 |
| 4 | 0 |
| 0 | 4 |
Etc.
Une fois tous ces tableaux trouvés, R calcule sur chacun une statistique et détermine ensuite combien rare est notre tableau de valeurs observées, comparé à tous ces tableaux possibles.
Cette procédure permet de toujours obtenir une valeur de p exacte, même quand les valeurs attendues sont < 5 ou < 1. C’est pourquoi certains auteurs recommandent de toujours utiliser ce test, car il serait bon en toutes circonstances. Cependant, avec de grands nombres dans le tableau, il devient extrêmement complexe à calculer, voir impossible pour un ordinateur ordinaire.
Le test de khi-carré lui a donc longtemps été préféré, parce qu’il est raisonnable à calculer manuellement, ce qui était très important il n’y a même pas 20-30 ans. Le test exact de Fisher serait aussi un peu moins puissant (plus conservateur) et pourrait donc, dans certaines circonstances, rater des liens significatifs que le test de khi-carré aurait trouvés. J’accepterai pour le cours son utilisation, comme bon vous semble en remplacement du test de khi-carré.
Dans R, le test exact de Fisher s’utilise exactement de la même façon que le khi-carré, soit en lui passant une matrice de données :
fisher.test(ma_matrice)
Fisher's Exact Test for Count Data
data: ma_matrice
p-value = 1
alternative hypothesis: two.sidedOn obtient donc avec ce test aussi une valeur de p de 1. Le test de Fisher ne trouve donc pas non plus d’association significative entre nos deux variables.